Page 87 - 《振动工程学报》2025年第9期

第 9 期 刘 豪，等：简支梁桥走行车桥系统的实时混合试验稳定性预测方法 2017

−8
×10 1.05×β Cri 1.025×β Cri 1×β Cri 0.975×β Cri 0.95×β Cri
4
加速度 / (m·s −2 ) −2 2 0

−4
0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8
t / s
(a) 界面加速度
(a) Interface acceleration
1.02

1.01
ρ (A i )
−
1.00
0.99
0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8
t / s
(b) 谱半径
(b) Spectral radius
10 2
第一跨 第二跨 第三跨 第四跨 第五跨
10 1
P i
10 0

0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8
t / s
(c) 累乘状态转移矩阵的谱半径
(c) Spectral radius of accumulated state transition matrixes

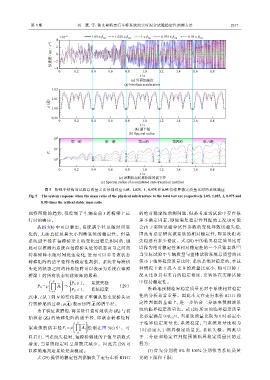
图 5 物理子结构与试验总质量之比分别对应 1.05、1.025、1、0.975 和 0.95 倍临界稳定质量比时的系统响应
Fig. 5 The system response when the mass ratio of the physical substructure to the total test are respectively 1.05, 1.025, 1, 0.975 and
0.95 times the critical stable mass ratio

观察图像的趋势，仅绘制了车辆在前 5 跨桥梁上运 的绝对稳定性预测问题，但是考虑到试验中存在很
行时的响应。 多不确定因素，即便满足稳定性判据的工况也可能
从图 5(b) 中可以看出，系统谱半径是随时间变 会由于实际试验中试件参数的变化导致试验失稳，
化的，无法直接从其大小判断系统的稳定性。但是 因此有必要研究该系统的相对稳定性，即系统距离
系统谱半径在每跨桥梁上的变化过程是相同的，因 失稳还有多少裕度。式 (28) 中的临界稳定质量比可
此可以推测出系统在每跨桥头处的状态向量之间的 以作为绝对稳定性和相对稳定性的一个具体表现 [19] ，
转移矩阵不随时间发生变化，进而可以参考该状态 当实际试验中车辆质量与整体试验系统总质量的比
转移矩阵的谱半径作为稳定性判据。系统在每跨桥 值小于临界稳定质量比时，系统是绝对稳定的，在这
头处的状态之间的转移矩阵可以表示为系统在整跨 种情况下若工况 A 比 B 的质量比更小，则可以称工
桥梁上的所有状态转移矩阵的累乘： 况 A 比 B 具有更高的稳定裕度，更容易在实际试验
  
N 中保持稳定性。

∏  P 0 ⩾ 1， 系统失稳
  
  （29）
P 0 = ρ   A i ⇒ 

   P 0 < 1， 系统稳定 准确地预测临界稳定质量比对于系统相对稳定

i=1
式中，i 从 1 到 N 的变化描述了车辆从简支梁桥头运 性的分析非常重要。因此本文在走行车桥 RTHT 稳
行到桥尾的过程；ρ(A i ) 表示矩阵 A i 的谱半径。 定性判据的基础上，进一步结合二分法来预测该系
为了验证该猜想，将系统任意时刻状态 (Z k ) 与初 统的临界稳定质量比。式 (28) 所示的临界稳定质量
始状态 (Z 0 ) 的转移矩阵的谱半径，即状态转移矩阵 比必定满足 0<β Cri <1，当系统质量比取为 0 时必定小
 k  于临界稳定质量比，系统稳定；当系统质量比取为
∏  

累乘值的谱半径 P i = ρ    A i绘制在图 5(c) 中。可


  1 时必定大于临界稳定质量比，系统失稳。因此基
0
以看出，当系统失稳时，每跨桥墩处的 P 值呈指数式 于二分法和稳定性判据预测临界稳定质量比的过
增加，当系统稳定时呈指数式减少。因此式 (29) 可 程为：
以准确地判定系统是否稳定。 (1) 首先分别将 0% 和 100% 分别作为系统质量
式 (29) 提供的稳定性判据解决了走行车桥 RTHT 比的上限和下限；