Page 86 - 《振动工程学报》2025年第9期

2016 振 动 工 程 学 报 第 38 卷

表 1 基于原型车 CRH 380A 简化的四分之一车模型参数 状态空间方程，可以描述车辆在多跨铁路桥梁上持
Tab. 1 Simplified quarter car model parameters based on 续运行的实时混合试验的状态变化。

prototype CRH 380A

参数 数值 3 走 行 车 桥 实 时 混 合 试 验 系 统 的 稳 定 性
m c /kg 33786
分 析 方 法
−1
k c /(kN·m ) 900
−1
c c /(kN·s·m ) 40
m b /kg 4112 对于线性时不变系统，可以根据其离散状态转
−1
k b /(kN·m ) 7088 移矩阵的谱半径 [28] 来判断系统稳定性，若谱半径大
−1
c b /(kN·s·m ) 80 于 1 则系统失稳，反之则系统稳定。然而由式 (27)
m w /kg 5068
可以看出，走行车桥 RTHT 系统的状态转移矩阵随

0.4 时间发生变化，这意味着该系统的谱半径也随时间

加速度 / (m·s −2 ) −0.2 0 判断该系统的稳定性。 RTHT 系统的稳定性与其谱
变化，无法直接使用线性时不变系统的稳定性理论
0.2
为了研究走行车桥
−0.4 半 径 之 间 的 关 系， 本 文 基 于 式 (27) 进 行 了 仿 真 分
0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 析。其中车辆和桥梁参数与 2.4 节中的参数相同，振
时间 / s
动台加载误差取 40 ms 的时滞误差，仿真的积分步长
×10 −4
0 取 1 ms。
子结构迭代求解
−2 状态空间方程求解 为了能够具体描述走行车桥 RTHT 系统的稳定
位移 / m −4 性，本文采用了临界稳定质量比 [18] 的概念，当实际的
−6 车辆质量与车桥总质量的比值 β 超出临界稳定质量
i
−8 比 β Cr 时系统将会失稳，若小于临界稳定质量比则系
0 0.05 0.10 0.15 0.20 0.25 0.30 0.35
时间 / s 统稳定。临界稳定质量比的计算如下式所示：

M Cri
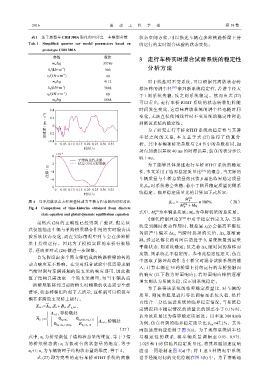
图 4 基于离散状态方程和整体动力平衡方程求解的时程对比 β Cri = P ×100% （28）
M Cri + M N
Fig. 4 Comparison of time-histories obtained from discrete P
式中， M 为车辆总质量；M N 为单跨桥梁的总质量。
Cri
state equation and global dynamic equilibrium equation P
[28]
《现代控制理论》 中对于稳定性定义为：当系
虽然式 (26) 的正确性已经得到了验证，但是该
统受到瞬时扰动作用时，被控量 x c (t) 会偏离平衡位
式仅能描述车辆与单跨桥梁耦合作用的实时混合试
置而产生偏差 Δx c ，当瞬时扰动消失后，Δx c 逐渐衰
验系统状态变化，而在实际情况中列车会在多跨桥
减，经过足够长的时间后趋近于 0，系统恢复到原来
梁上持续运行。因此为了模拟实际的车桥行驶场
平衡状态，则系统稳定；反之若 Δx c 随时间的推移而
景，还需要对式 (26) 做进一步调整。
发散，则系统是不稳定的。参考此稳定性定义，仿真
首先假设由多个简支梁组成的铁路桥梁的各跨
中选取了脉冲荷载作为车桥实时混合试验系统的输
动力响应互不影响。在实时混合试验中仅需要求解
入，计算车辆在 30 跨桥梁上持续运行的车桥接触面
当前时刻与车辆接触的简支梁的响应即可，因此数
的响应 (以下称为界面响应)，若界面响应峰值逐渐
值子结构只需选取一个简支梁模型，每当车辆从前
增大则认为系统失稳，反正则系统稳定。
一跨桥尾转移到当前跨桥头时桥梁的状态需要全部
为了获得该系统的临界稳定质量比，对车辆的
清零，状态转移矩阵如下式所示，这样就可以模拟车
质量、刚度和阻尼进行等比调幅至系统失稳，然后
辆在多跨简支梁桥上运行。
再结合二分法逼近系统的临界稳定情况，当系统稳
Z i+1 =A i+1 Z i + B i+1 F g,i+1 ，
定情况和不稳定情况的质量比的误差小于 0.1% 时，

 A i+1 , 非桥墩处
 认为该质量比为临界稳定质量比。以车速
 [ ] 300 km/h

A i+1 = 0 n b ×n b 0 n b ×(n t +n v +3)
 A i+1 , 桥墩处

 为例，仿真得到的临界稳定质量比 β Cri =47.1%。其界
0 (n t +n v +3)×n b E n t +n v +3
（27） 面加速度响应绘制于图 5(a)。为了观察系统谱半径
式中，n b 为桥梁数值子结构状态量的维度，等于 3 倍 与 稳 定 性 的 联 系， 将 车 辆 质 量 调 幅 至 0.95、 0.975、
的桥梁模态数；n t 为振动台的状态量的维度，等于 1.025 和 1.05 倍临界稳定质量比，将其界面加速度响
n d +1；n v 为车辆物理子结构状态量的维度，等于 4。 应也一同绘制在图 5(a) 中；将上述 5 种情况中系统
式 (27) 即为完整的走行车桥 RTHT 系统的离散 谱半径随时间的变化绘制在图 5(b) 中。为了清晰地