Page 88 - 《振动工程学报》2025年第9期

2018 振 动 工 程 学 报 第 38 卷

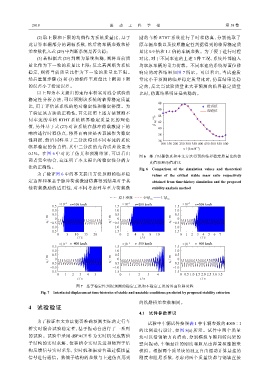
(2) 取上限和下限的均值作为系统质量比，基于 励的车桥 RTHT 系统进行了时程仿真，分别选取了
此计算车辆部分的调幅系数，然后将车辆参数和桥 原车辆参数以及按照稳定性判据得到的临界稳定质
梁参数代入式 (29) 中判断系统是否失稳； 量比 0.9 倍和 1.1 倍的车辆参数。为了便于进行时程
(3) 若根据式 (29) 判断为系统失稳，则将当前质 对比，对于不同车速的上述 3 种工况，系统外部输入
量比作为下一轮的质量比上限；反之若判断为系统 均取原车辆的重力荷载。不同车速的系统界面位移
稳定，则将当前质量比作为下一轮的质量比下限。 响应的时程结果如图 7 所示。可以看出，当试验质
然后重复步骤 (2) 和 (3) 的操作至质量比上限和下限 量比小于预测的临界稳定质量比时，仿真结果是稳
的误差小于指定误差。 定的，反之当试验质量比大于预测的临界稳定质量
以上即为本文提出的走行车桥实时混合试验的 比时，仿真结果明显是失稳的。
稳定性分析方法，可以预测该系统的临界稳定质量

48
比，用于评估该系统的绝对稳定性和稳定裕度。为 仿真值
46 理论值
了验证该方法的正确性，首先按照上述方法预测不 44
同 车 速 的 车桥 RTHT 系 统 临 界 稳 定 质 量 比 的 理 论 β Cri / % 42
值，另外基于式 (27) 对该系统在脉冲荷载激励下的
40
响应进行时程仿真，将界面响应是否衰减作为稳定 38
性判据，然后同样基于二分法得到不同车速的系统 36
100 150 200 250 300 350 400 450 500 550 600
临界稳定的仿真值，其中二分法的允许误差设置为 v / (km·h )
−1

0.1%。在图 6 中对比了仿真和预测结果，可以看出
图 6 基于时程仿真和本文方法得到的临界稳定质量比的仿
两者完全吻合，这证明了本文提出的稳定性分析方
真值和理论值对比
法的正确性。
Fig. 6 Comparison of the simulation values and theoretical
为了验证图 6 中的本文提出方法预测的临界稳 values of the critical stable mass ratio respectively
定边界和和基于脉冲荷载激励仿真得到结果对于其 obtained from time-history simulation and the proposed
他荷载激励的适用性，对不同考虑列车重力荷载激 stability analysis method

原车参数 0.9β Cri 1.1β Cri

1.5 ×10 −3 v=100 km/h 1.5 ×10 −3 v=200 km/h 1.5 ×10 −3 v=300 km/h
1.0 1.0 1.0
0.5 0.5 0.5
x I / m −0.5 0 x I / m −0.5 0 x I / m −0.5 0
−1.0 −1.0 −1.0
−1.5 −1.5 −1.5
0 5 10 15 20 0 2 4 6 8 10 0 1 2 3 4 5 6 7
t / s t / s t / s
1.5 ×10 −3 v=400 km/h 1.5 ×10 −3 v=500 km/h 1.5 ×10 −3 v=600 km/h
1.0 1.0 1.0
0.5 0.5 0.5
x I / m −0.5 0 x I / m −0.5 0 x I / m −0.5 0

−1.0 −1.0 −1.0
−1.5 −1.5 −1.5
0 1 2 3 4 5 0 1 2 3 4 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
t / s t / s t / s

图 7 基于稳定性判据预测的稳定工况和不稳定工况的界面位移时程
Fig. 7 Interfacial displacement time-histories of stable and unstable conditions predicted by proposed stability criterion

的铁路桥梁参数相同。

4 试 验 验 证
4.1 试件参数辨识
为了验证本文方法能否准确预测实际的走行车 试验中车辆试件按照表 1 中车辆参数的 4000∶1
桥实时混合试验稳定性，基于振动台进行了一系列 的比例进行设计，如图 8(a) 所示。试件中两个质量
的试验。试验中采用 dSPACE 作为实时机完成数值 块可以沿钢轴方向滑动，分别模拟车厢和转向架的
子结构的实时求解、位移指令实时发送和物理子结 竖向振动，车辆悬挂的刚度和阻尼由弹簧和摩擦来
构反馈信号实时采集，实时机和振动台通过模拟量 模拟。根据两个质量块的独立自由振动计算悬挂的
信号进行通信。数值子结构的参数与上述仿真用到 刚度和阻尼系数，考虑到两个质量块都与钢轴直接