Page 110 - 《振动工程学报》2025年第9期

速度
−5
−10
ω
速度
−5
−10
−5
位移
ω
速度
−5
−5
位移
ω
速度
−5 −5 混沌 位移 混沌
−10
2040 −5 振 动 工 程 学 报 第 38 卷
位移
(d) ω=0.966

4
6 T=8 T=4 T=2 P AS1
3
混沌吸引子 x 1 2 T=1
4
1 混沌 T=1
速度x 1 2 0
·
TLE −0.5
0
−1.0
0.9 1.0 1.1 1.2 1.3
−2
3.0 3.5 4.0 4.5 ω
(a) 正扫频(0.9<ω<1.3)
位移x 1
(a) Forward sweep frequency(0.9<ω<1.3)
(e) ω=0.966
4
6
T=8 T=4 T=2
P AS2
3
4 x 1 2 T=1
P -混沌吸引子
AS2
1
速度x 1 2 AS1 0
· P -混沌吸引子 混沌 T=1
TLE −0.5
0
−1.0
0.9 1.0 1.1 1.2 1.3
−2
3.0 3.5 4.0 4.5 ω
位移x 1 (b) 倒扫频(0.9<ω<1.3)
(f) ω=0.955 (b) Backward sweep frequency(0.9<ω<1.3)

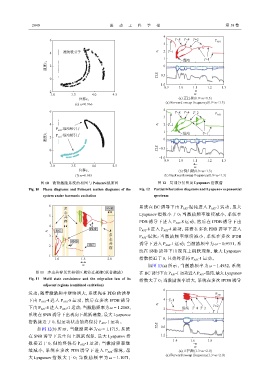
图 10 简谐激励系统的相图与 Poincaré截面图 图 12 局部分岔图及 Lyapunov 指数谱
Fig. 10 Phase diagrams and Poincaré section diagrams of the Fig. 12 Partial bifurcation diagrams and Lyapunov exponential
system under harmonic excitation spectrum

6 系统在 BC 诱导下由 P AS2 -混沌进入 P AS2 -1 运动，最大
多 SNB
态 指数小于 0；当激励频率继续减小，系统在
5 共 Lyapunov
存 PDB 诱导下进入 P AS2 -8 运动，然后在 IPDB 诱导下由
4
PDF P AS2 -8 进入 P AS2 -4 运动，接着在多次 PDB 诱导下进入
x 1 BC
3 多 P AS2 -混沌；当激励频率继续减小，系统在多次 IPDB
态
SNB
2 BC 共 诱导下进入 P AS2 -1 运动；当激励频率为 ω = 0.9331，系
存
统在 SNB 诱导下出现向上跳跃现象，最大 Lyapunov
1
1.0 1.5 2.0 指数接近于 0，且始终保持 P AS2 -1 运动。
ω 如图 13(a) 所示，当激励频率为 ω = 1.4932，系统

图 11 多态共存及其相邻区域转迁规律（联合激励） 在 BC 诱导下由 P AS1 -1 运动进入 P AS1 -混沌，最大 Lyapunov
Fig. 11 Multi state coexistence and the migration law of its 指数大于 0；当激励频率增大，系统在多次 IPDB 诱导
adjacent regions (combined excitation)

6
运动；随着激励频率继续增大，系统先在 PDB 的诱导 P AS1
下由 P AS1 -4 进入 P AS1 -8 运动，然后在多次 IPDB 诱导 4 T=1
x 1
下由 P AS1 -8 进入 P AS1 -1 运动；当激励频率为 ω = 1.2168， 2 混沌 T=4 T=2 T=2
T=1
系统在 SNB 诱导下出现向下跳跃现象，最大 Lyapunov
0
指数接近于 0，但运动状态始终保持 P AS1 -1 运动。
如图 12(b) 所示，当激励频率为 ω = 1.1715，系统 TLE −0.6
在 SNB 诱导下发生向上跳跃现象，最大 Lyapunov 指 −1.2
1.4 1.6 1.8
数接近于 0，但始终保持 P AS2 -1 运动；当激励频率继
ω
续减小，系统在多次 PDB 诱导下进入 P AS2 -混沌，最 (a) 正扫频(1.3<ω<2.0)
(a) Forward sweep frequency(1.3<ω<2.0)
大 Lyapunov 指 数 大 于 0； 当 激 励 频 率 为 ω = 1.1071，
混沌
混沌

−0.6
−1.2

ω
倒扫频 ω
ω