Page 109 - 《振动工程学报》2025年第9期

第 9 期 屈鸣鹤，等：含常数激励的分数阶非线性隔振系统幅频特性及周期运动多样性研究 2039

P AS2 -1 P AS2 -2 Lyapunov 指数谱（TLE）。
4 如图 12(a) 所 示 ， 当 激 励 频 率 为 ω = 0.9， 系 统 为
P AS3 -1 P AS3 -2
P AS2 -1
P AS1 -1 运动，最大 Lyapunov 指数小于 0；当激励频率
P AS3 -混沌 为 ω = 0.9644，系统在 BC 诱导下由 P AS1 -1 运动进入 P AS1 -
x 1 3 双态
共存 混沌，最大 Lyapunov 指数大于 0；当激励频率 ω继续
P AS2 -混沌
增大，系统在多次 IPDB 诱导下由 P AS1 -混沌进入 P AS1 -4
P AS1 -1
2 三态共存 10

0.82 0.83 0.84 0.85 0.86
5
ω
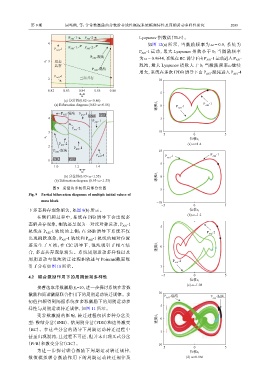
(a) 分岔图(0.82<ω<0.86)
· P -1
(a) Bifurcation diagram (0.82<ω<0.86) 速度x 1 0 P AS1 -1 AS2
P AS2 -混沌 P AS2 -1
SNB PFB
4 −5
P AS1 -1
P AS1 -2
3 −10 −5 0 5
x 1
位移x 1
P AS1 -2 (a) ω=1.4
2 P AS1 -1
P AS1 -混沌 10
P AS2 -1 P -1 P AS2 -1
CIC PDB AS1
1
5
1.0 1.2 1.4
ω
·
(b) 分岔图(0.95<ω<1.55) 速度x 1 0
(b) Bifurcation diagram (0.95<ω<1.55)

图 9 质量块多初值局部分岔图 −5
Fig. 9 Partial bifurcation diagrams of multiple initial values of
mass block −10
−5 0 5
下多态共存现象消失，如图 9(b) 所示。 位移x 1
(b) ω=1.2
在倒扫频过程中，系统在 PFB 诱导下会出现多
态解共存现象，相轨迹呈现为一对反对称运动，P AS1 -1
5
轨线在 P AS2 -1 轨线的上侧；在 SNB 诱导下系统不仅 P -2
AS2
出现跳跃现象，P AS1 -1 轨线和 P AS2 -1 轨线的相对位置
还发生了互换；在 CIC 诱导下，混沌吸引子相互结 · 速度x 1 0
合，多态共存现象消失。系统周期运动多样性以及
周期运动与混沌转迁过程相轨迹与 Poincaré截面吸 P -2
AS1
引子分布如图 10 所示。 −5

4.2 联合激励作用下的周期运动多样性 −5 0 5
位移x 1
(c) ω=1.08
接着选取常数激励 f 0 =10，进一步探讨系统在常数
激励和简谐激励联合作用下的周期运动转迁规律。多 10 P -混沌
AS1 P AS2 -混沌
初值扫频得到隔振系统在多源激励下的周期运动多
5
样性与周期运动转迁规律，如图 11 所示。
受常数激励的影响，转迁过程包括多种分岔类 ·
型：鞍结分岔（SNB）、倍周期分岔（PDB）和边界激变 速度x 1 0
（BC）。在这些分岔的诱导下周期运动转迁过程中 −5
甚至出现混沌，且过程不可逆，但并未出现叉式分岔
（PFB）和激变分岔（CIC）。 −10
−5 0 5
为进一步探讨联合激励下周期运动转迁规律，
位移x 1
数值模拟联合激励作用下的周期运动转迁规律及 (d) ω=0.966

混沌吸引子

速度

−2
位移
ω

混沌吸引子
混沌吸引子
速度

−2
位移
ω