Page 105 - 《振动工程学报》2025年第9期

第 9 期 屈鸣鹤，等：含常数激励的分数阶非线性隔振系统幅频特性及周期运动多样性研究 2035

p
式中， D [X 1 (T)]为分数阶微分项，是 X 1 (T) 关于时间 K e 分别为：
q
T
T 的 p 阶导数 （0 ⩽ p ⩽ 1）。 C eq = 2ξ +α （9）
引入无量纲参数 F s ，进行如下变量代换： K eq = 1+µ k +β （10）
√ √
M C
K 1 K 1 由式 (9) 和 (10) 可知，不同的分数阶系数 λ和分
x i = X i ，t = T ，ω = Ω ，ξ = √ ，
F s M K 1 2 K 1 M 数阶阶数 p 会改变系统的等效线性刚度系数 K e 和
q
F K
K 2 F 0 K 3 2
µ k = ， f = ，f 0 = ，ε = F ，λ = 。 等效阻尼系数 C eq 。为进一步探索分数阶阶数 在不
s
K 3 p
K 1 F s F s 1 K 1
q
将上述参数代入式 (1) 可得： 同频率范围内对系统等效刚度系数 K e 和等效阻尼
{ 3 p 系数 C e 的影响，以频率 ω = 1为界限探讨分数阶阶
q
¨ x 1 +(1+µ k )x 1 − x 2 +εx +λD [x 1 (t)] = f 0 + f cos(ωt)
t
1
2ξ ˙x 2 + x 2 − x 1 = 0 数 p 在不同频率范围内的影响规律。
（2） 下面分别对系统的等效线性刚度系数 K e 和等
q
式 中， D [x 1 (t)]为 参 数 变 换 后 的 分 数 阶 微 分 项 ， 是 效 阻 尼 系数 C e 进 行 研 究 。 选 取 系 统 参 数 ξ = 0，
p
t
q
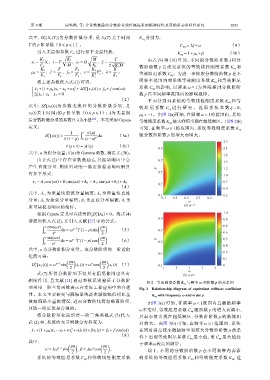
x 1 (t)关于时间 t的 p 阶导数 （0 ⩽ p ⩽ 1） λ为无量纲 µ k = −1。由图 2(a)可知，在频率 ω < 1的范围内，系统
；
后分数阶微分项的系数且 λ为小量 [22] 。本文采用 Caputo 等效刚度系数 K e 最大峰值出现在超低频区。由图 2(b)
q
定义： 可知，在频率 ω ⩾ 1的范围内，系统等效刚度系数 K eq
1 w t x (u)
′
p
D [x(t)] = p du （3a） 随分数阶阶数 p 的增大而增大。
t
Γ(1− p) 0 (t −u)
2.3
Γ(y+1) = yΓ(y) （3b）
0.9 2.1
式中，u 为积分变量； Γ(n)为 Gamma 函数，满足式 (3b)。
1.8
由于式 (2) 中存在常数激励 f 0 ，其振动响应中会 0.7
1.5
产生直流分量，则质量块的一阶近似稳态响应解具 p 1.2
有如下形式： 0.5 1.0
x 1 = A 1 cos(ωt)+ B 1 sin(ωt)+ A 0 = A 11 sin(ωt +θ 1 )+ A 0 0.3 0.7
（4）
0.4
式中，A 1 为质量块谐波分量幅值；A 0 为质量块直流
1
0.1 0.2
分量；A 1 为余弦分量幅值；B 1 为正弦分量幅值；θ 1 为 0.1 0.3 0.5 ω 0.7 0.9
质量块稳态响应的相位。 (a) ω<1
p
根据 Caputo 定义可直接得到 c a D [A 0 ] = 0。将式 (4) 1.0
t
0.9 0.9
谐波项代入式 (2)，并引入文献 [27] 中的公式：
w t cos(ωs) ( pπ ) 0.8
ds = ω p−1 Γ(1− p)sin （5） 0.7
0 s p 2 0.6
w t sin(ωs) ( pπ )
ds = ω p−1 Γ(1− p)cos （6） p 0.5 0.5
0 s p 2
0.4
式中，s 为分数阶积分变量。取分数阶项的一阶近似
0.3 0.3
化简可得：
0.1
( pπ ) ( pπ )
p
p
D [x 1 (t)] ≈ ω p−1 sin ˙ x 1 (t)+ω cos x 1 (t) （7） 0.1 0
t
2 2 1 3 5 7 9
式 (7) 所得分数阶项不仅具有阻尼作用也具有 ω
(b) ω≥1

刚度作用，且文献 [11] 通过参数识别验证了分数阶
图 2 等效刚度系数 K e 与频率 ω 和阶数 p 的关系图
q
项采用一阶三角函数表示在实际工程应用中的合理 Fig. 2 Relationship diagram of equivalent stiffness coefficient
性。本文主要研究与隔振系统高次谐波幅值相比基 K eq with frequency ω and order p

波幅值是小量的情况，进而分数阶化简忽略高阶项， 由图 3(a) 可知，在频率 ω < 1范围内且激励频率
只取一阶近似是合理的。 ω不变时，等效阻尼系数 C e 随阶数 p 的增大而减小，
q
将分数阶项化简所得一阶三角函数式 (7) 代入 其最小值出现在超低频区，分数阶阶数 p 的数值相
式 (2) 中，系统的无量纲微分方程变为： 对较大。由图 3(b) 可知，在频率 ω ⩾ 1范围内，系统
3
¨ x 1 +(1+µ k )x 1 − x 2 +εx +α˙x 1 (t)+βx 1 (t) = f 0 + f cos(ωt) 在同时满足较小激励频率和较大分数阶阶数 p 的条
1
（8） 件下出现等效阻尼系数 C e 最小值，而 C e 最大值处
q
q
其中：
( pπ ) ( pπ ) 于频率 ω较高的频带。
α = λω p−1 sin ， β = λω cos 。 综上，不同的分数阶阶数 在不同频带内会影
p
2 2 p
系统的等效阻尼系数 C e 和等效线性刚度系数 响系统的等效阻尼系数 C e 和等效刚度系数 K eq ，进
q
q