Page 106 - 《振动工程学报》2025年第9期

2036 振 动 工 程 学 报 第 38 卷

{[ ] }
1.0 ( ) 3a 2 3b 2
2
2
2
2
2
6ξ a +b ω +a + 1 + 1
a 0 1 1 0 ε+β+µ k = f 0
0.9 0.9 2 2
（16）
0.7
0.7 其中：
0.6
a 2 b 2
( 2 2 ) 2 2 1 1
2
1
1
p 0.5 ψ 1 = ξ a +b ω +a + + ，
0
0.5 4 4
0.4 α
ψ 2 = (β+µ k +1)ξ + 。
2
0.2
0.3 联立式 (14)~(16) 可求解出节点的一阶近似解的
0.1
直流分量和谐波响应幅值，再将节点近似解代入式 (12)
0.1 0
0.1 0.3 0.5 0.7 0.9 中，可得到质量块的稳态响应解。
ω
(a) ω<1 随机选取一组系统参数，采用一阶谐波平衡法
2.4 可得系统的幅频响应解，系统在联合激励作用下的
0.9 2.1 幅频响应解为谐波分量与直流分量之和，其中谐波
1.8 分量为简谐激励作用下的稳态响应解，直流分量为
0.7 1.5 常数激励作用下的稳态响应解，如图 4 所示。

p 1.2
0.5 8
0.9 骨架线
0.6
0.3 6
0.3
0.1 0 质量块谐波分量幅值A 11 4
1 3 5 7 9
ω
(b) ω≥1
2
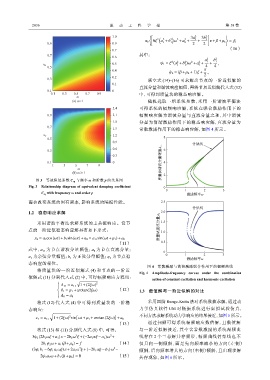
图 3 等效阻尼系数 C e 与频率 ω 和阶数 p 的关系图
q
Fig. 3 Relationship diagram of equivalent damping coefficient 0
0 1 2 3
C eq with frequency ω and order p 激励频率ω
而会改变系统的固有频率，影响系统的隔振性能。 2.5

骨架线
1.2 稳态响应求解
质量块直流分量A 0 2.0
采用谐波平衡法求解系统的主共振响应。设节 1.5
点的一阶近似稳态响应解具有如下形式： 1.0
x 2 = a 1 cos(ωt)+b 1 sin(ωt)+a 0 = a 11 sin(ωt +φ 1 )+a 0
（11） 0.5
式中，a 1 为节点谐波分量幅值；a 0 为节点直流分量；
1
0
a 1 为余弦分量幅值；b 1 为正弦分量幅值；φ 1 为节点稳 0 1 2 3
激励频率ω
态响应的相位。
图 4 常数激励与简谐激励联合作用下的幅频曲线
将质量块的一阶近似解式 (4) 和节点的一阶近
Fig. 4 Amplitude-frequency curves under the combination
似解式 (11) 分别代入式 (2) 中，可得幅频响应方程组：
action of constant excitation and harmonic excitation
 √
 A 11 = a 11 1+(2ξω) 2



 （12）
 θ 1 = φ 1 +arctan(2ξω) 1.3 数值解与一阶近似解的对比




A 0 = a 0
将式 (12) 代入式 (4) 中可得到质量块的一阶稳 采用四阶 Runge-Kutta 法对系统数值求解，通过动
态响应： 力学仿真软件 UM 对隔振系统进行虚拟试验仿真，
√
2 [ ] 不同方法求解系统动力学响应的结果接近，如图 5 所示。
x 1 = a 11 1+(2ξω) sin ωt +φ 1 +arctan(2ξω) +a 0
（13） 通过扫频可得系统幅频响应数值解，且数值解
将式 (13) 和 (11) 分别代入式 (8) 中，可得： 与一阶近似解接近，其中含常数激励的系统幅频曲
2
3
3ψ 1 (2b 1 ωξ +a 1 )ε−2b 1 ω ξ +(−2a 1 αξ −a 1 )ω + 线存在 2 个三态解共存频带，幅频曲线骨架线也不
2b 1 ψ 2 ω+a 1 (β+µ k ) = f （14） 仅只向一侧倾斜，而是先向频率减小的方向（左侧）
3 2
(3ψ 1 b 1 −6ψ 1 a 1 ωξ)ε+2a 1 ω ξ +(−2b 1 αξ −b 1 )ω − 倾斜，后向频率增大的方向（右侧）倾斜，且出现多解
2ψ 2 a 1 ω+b 1 (β+µ k ) = 0 （15） 共存现象，如图 6 所示。