Page 107 - 《振动工程学报》2025年第9期

第 9 期 屈鸣鹤，等：含常数激励的分数阶非线性隔振系统幅频特性及周期运动多样性研究 2037

4 8

RK4 UM仿真 HB
三解共存
RK4
2 6 UM
位移x 1 0 2.5 质量块振幅A 骨架线 上支

2.0 4 左中支 右中支
−2 右下支
1.5 左下支
80 90 100
−4 2
0 50 100 150 200 0 1 2 3
时间t 激励频率ω

(a) ω=1
图 6 不同方法求解系统的幅频曲线
4 Fig. 6 Amplitude-frequency curves of system solved by
RK4 UM仿真
different methods
3
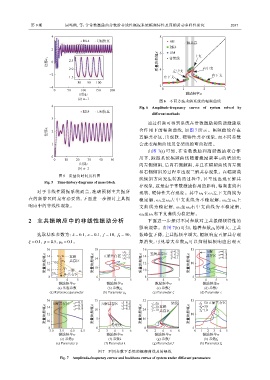
通过扫频可得到系统在常数激励和简谐激励联
位移x 1 2 合作用下的幅频曲线，如图 7 所示。幅频曲线存在
五解共存区，出现软、硬特性共存现象，而不同参数
1 会改变幅频曲线及骨架线的弯曲程度。
由图 7(a) 可知，在常数激励和简谐激励联合作
0 用下，隔振系统幅频曲线随着激励频率 ω的增加先
0 10 20 30 40 50
时间t 向左侧倾斜，后向右侧倾斜，并且在幅频曲线向左侧
(b) ω=2
和右侧倾斜的过程中出现三解共存现象。在幅频曲

图 5 质量块时间历程图
线倾斜方向发生转换的过程中，甚至还出现五解共
Fig. 5 Time-history diagrams of mass block
存现象，这是由于常数激励作用的影响，幅频曲线出
对于非线性隔振系统而言，准确预测主共振所 现软、硬特性共存现象。其中 ω 0 至 ω 1 左下支曲线为
在的频带区间是有必要的，下面进一步探讨主共振 稳定解， ω 1 至 ω 2 左中支曲线为不稳定解， ω 2 至 ω 3 上
响应中的非线性现象。 支曲线为稳定解， ω 3 至 ω 4 右中支曲线为不稳定解，

ω 4 至 ω 5 右下支曲线为稳定解。
2 主 共 振 响 应 中 的 非 线 性 振 动 分 析 下面进一步探讨不同参数对主共振幅频特性的
影响规律。由图 7(b) 可知，随着参数 µ k 的增大，主共
，
选取基准参数为： λ = 0.1 ε = 0.1 f = 10 f 0 = 50， 振峰值下降，主共振频率增大，幅频响应五解共存现
，
，
，
，
ξ = 0.1 p = 0.5 µ k = 0.1。 象消失，可见增大参数 µ k 可以抑制幅频响应出现五

16 18 16 15
ξ=0.3
μ k =1 14 五解共存区 ξ=0.2 五解 ε=0.1
μ k =3
质量块振幅A 12 ω 2 ω 4 ω 1 共存区 质量块振幅A 14 μ k =5 质量块振幅A 12 ξ=0.1 质量块振幅A 10 ε=0.5
ε=0.3
五解共存区
共存区
14
五解
ω 3
10
10
共存区
ω 0 三解 ω 5 10
8 6 8 5
3 4 5 3 4 5 3 4 5 3 4 5 6
激励频率ω 激励频率ω 激励频率ω 激励频率ω
(a) 基准参数 (b) 参数μ k (c) 参数ξ (d) 参数ε
(a) Reference parameter (b) Parameter μ k (c) Parameter ξ (d) Parameter ε
16 15 32 15
五解共存区 p=0.1 五解共存区 λ=0.1 f=50 架线 f 0 =50 五解共存区
p=0.5
质量块振幅A 12 质量块振幅A 10 5 质量块振幅A 24 f=10 共存区 质量块振幅A 10 f 0 =10
λ=0.2
f=30 五解
f 0 =30
14
λ=0.3
p=0.9
16
10
骨架线
8 0 8 5
3.0 3.5 4.0 4.5 2 3 4 5 6 0 2 4 6 8 0 1 2 3 4 5
激励频率ω 激励频率ω 激励频率ω 激励频率ω
(e) 参数p (f) 参数λ (g) 参数f (h) 参数f 0
(e) Parameter p (f) Parameter λ (g) Parameter f (h) Parameter f 0

图 7 不同参数下系统的幅频曲线及骨架线
Fig. 7 Amplitude-frequency curves and backbone curves of system under different parameters