Page 79 - 《振动工程学报》2025年第9期

第 9 期 朱前坤，等：结构三维形变的双目立体视觉鲁棒监测研究 2009

正，然后采用改进的基于相位 SGBM 算法计算校正 表 3 测试结果误差对比
后图像的视差信息，并计算各像素点的深度数据。 Tab. 3 Comparison of test result errors

然后，利用仿真试验优化的参数对位移数据进行拟 桥梁位置 RMSE/%
合，获得竖向位移时程曲线。最后，将计算所得位移 跨中挠度 1.7
时程曲线与激光位移传感器的测量曲线进行对比分 D点顺桥向应变 4.8
E点顺桥向应变 7.4
析，图 14 为激励稳定后 6 s 的测量对比数据。两种
方 法 所 得 位 移 变 化 趋 势 基 本 吻 合， 由 于 本 文 算 法
应变 / ε
对像素点进行追踪测量，能够更精细地捕捉结构的 4.068×10 −5
4.062×10 −5
微小变化，因此位移峰值稍高，导致所计算的位移 z / pixel 4.056×10 −5
−5
4.050×10
峰值略大于激光位移传感器所测数据，单点位移测 4.044×10 −5
4.039×10 −5
量的误差总体较小，为 1.7%，符合工程应用精度要求。 4.033×10 −5
x / pixel 4.027×10 −5
−5
4 y / pixel 4.021×10 −5
4.015×10
3 本文方法 激光位移计 4.009×10 −5
(a) 顺桥向应变云图
2 (a) Strain nephogram along the bridge
位移 / mm −1 1 0 应变 / ε −5
2.355×10
−2 2.351×10 −5
−5
2.347×10
−3 z / pixel 2.343×10 −5
−5
0 2 4 6 2.339×10 −5
2.335×10
时间 / s −5
2.332×10 −5
2.328×10
图 14 位移时程 x / pixel 2.324×10 −5
y / pixel 2.320×10 −5
Fig. 14 The displacement time-history −5
2.316×10
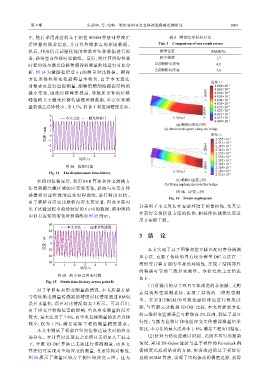
在得到位移场后，利用 SVR 算法和应变转换方 (b) 横桥向应变云图
(b) Strain nephogram cross the bridge
法得到感兴趣区域的应变场变化，提取与应变片传
图 16 应变云图
感器相对应位置的应变时程曲线，进行精度对比。
Fig. 16 Strain nephogram
由于顺桥向应变比横桥向应变更显著，因此主要对
分表明了本文算法在复杂环境下的鲁棒性，尤其是
比了试验过程中趋势较好的 6 s 内的数据，跨中顺桥
在获得全场信息方面的优势，相较传统视觉法更适
向 D 点应变的变化时程曲线如图 15 所示。
用于实际工程。

60
本文方法 应变片传感器
40
3 结 论
20
应变 / µε −20 0 本文实现了基于图像相位立体匹配时序分析测
−40 量方法，克服了传统的具有块分辨率 DIC 方法在三
−60
0 1 2 3 4 5 6 维形变计算方面的不足的局限性，实现了结构部件
时间 / s
的精确可靠的三维形变测量。本研究的主要结论

图 15 跨中 D 点应变时程
如下：
Fig. 15 Strain time-history across point D
（1）所提出的基于双目立体视觉的非接触、无靶

对于单目标点形变测量的情况，本文所提方法
点 结 构 形 变 监 测 系 统， 实 现 了 结 构 的 三 维 形 变 测
与传统形变测量传感器的精度对比情况通过 RMSE
量。在采用 PBGM 的可视化虚拟环境进行模拟试
误差来量化，误差对比情况如表 3 所示。可以看出，
验，与有限元分析和 3D-DIC 比较，本文所提出方法
由于应变片粘贴位置的影响，单点应变测量的误差
的三维形变监测误差可控制在 2% 以内，验证了其可
较大，最大达到了 7.4%，而单点位移测量的误差总体
行性；与激光位移计和电阻应变片传感器测量结果
较 小， 仅 为 1.7%， 满 足 实 际 工 程 的 测 量 精 度 要 求 。
本文中测试了桥梁在竖向位移达最大时的应变 相比，本方法的最大误差小于 8%，满足工程应用精度。
场分布。在计算时发现复杂光照且无明显人工标志 （2）针对自然纹理难以识别、光照不均匀的复杂
下，开源 3D-DIC 算法已无法进行准确测量，而本文 情况，采用 2D-Gabor 滤波与基于相位的 Farneback 稠
算法仍可实现对全场应变的测量，考虑结构对称性， 密梯度光流相结合的方法，配合改进的基于相位信
图 16 展示了测量区域左半侧区域应变云图。这充 息的 SGBM 算法，实现了结构振动的稠密追踪，获得