Page 77 - 《振动工程学报》2025年第9期

第 9 期 朱前坤，等：结构三维形变的双目立体视觉鲁棒监测研究 2007

有限元滑动窗口作为子区域，对子区域内的应变像 增加，测量误差趋于降低，但超过 30 pixel 后，会产生
素进行平均，即可产生与应变片测量相当的应变结 过度拟合导致误差放大，因此确定最佳拟合步长为
果。相较于应变片方法，有限元滑动窗法提高了对 30 pixel，测量误差为 0.025。
局部应变分布的采样密度，可灵活选择子区域的位
置，实现对整个感兴趣区域的全场应变测量，获得连 真实形变值
续应变场。 有限元模型 评估
耦合 有限元变形 等效变形

立体视觉测量
2 试 验 设 计 和 数 据 处 理
形变图像信息
基于物理图形模型 变形可视化
本 文 通 过 均 方 根 误差 (RMSE) 和 误 差 面 积 比 虚拟环境 Z
(EAR) 评估所涉及到的算法测量精度，分别表示为： ROI B X Y
v
u
t t 2 Y X 双目相机测量系统 A B
u r ∑(
)
c
σ −σ i Z 模拟光源
i
i=1
RMSE = （22）
r
式中， σ 为本文方法测量的数据； σ 为参考数据，r 为 图 8 算法评估框架
t
c
i i
数据个数。 Fig. 8 Algorithm evaluation framework
∑
1(∈ i > E t ) 以有限元分析获得的形变数据作为参考数据，
i∈P
EAR = （23） 将本文方法与 3D-DIC 方法进行精度比较，并通过误
P
{
1 ，if x is true 差对比进行定量分析，为进一步优化所提方法的参
式 中， 1(·) 为 指 标 函 数 ； 1(x) = ∈ i 表
0，if x is false 数提供直观参考。

示第 i 个像素点的位移/应变测量的误差值； E t = 0.015×
2.1.2 结果分析
[ ]
(max(g)−min(g) ，其中 g 表示位移/应变真值；P 为像
在获得的结构变形图像中分别选取第二跨和第
素总数。
三跨跨中 1200×360 pixel 大小的感兴趣区域用于分

2.1 基于 PBGM 虚拟现实技术模拟试验 析。通过开源 3D-DIC [18] 程序和本文所提方法对其
进行分析，得到的 A、B 点的位移和应变时程，通过
2.1.1 试验设计 与有限元分析所得的真值进行对比，误差分析如表 1
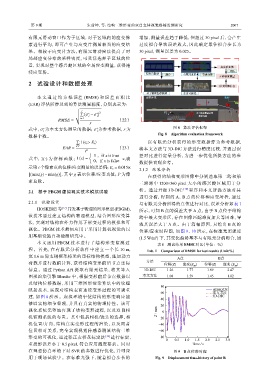
HOSKERE 等 [17] 开发基于物理的图形模型 (PBGM)， 所示，可知 B 点的误差大于 A 点，由于 B 点位于结构
该技术通过建立结构的物理模型，结合图形渲染算 跨中最大变形区，存在图像匹配难度加大等困难，导
法，实现对结构在外力作用下形变过程的模拟和可 致其误差大于 A 点。由于篇幅原因，只给出 B 点的
视化。PBGM 技术最初应用于采用计算机视觉的民
位移/应变时程图，如图 9、10 所示，在标准光照强度
用基础设施自动检测研究中。 (1.5 W/m ) 下，其变化趋势基本与有限元分析吻合，因
2
本 文 运用 PBGM 技 术 进 行 了 结 构 形 变 监 测 过 表 1 测试结果 RMSE 对比（单位：%）
程。首先，在有限元分析软件中建立一个长 10 m， Tab. 1 Comparison of RMSE for test results (Unit:%)

宽 1.6 m 简支钢框架桥梁的目标结构模型，施加动力 A点 B点
荷载并进行数值计算，获得结构变形前后节点坐标 方法 位移(Z) 应变(E yy ) 位移(Z) 应变 (E yy )
信息。通过 Python API 提取有限元结果，将其导入 3D-DIC 1.26 1.77 1.69 2.47
图形渲染引擎 Blender 中，根据变形前后节点数据以 本文方法 1.08 1.59 1.45 1.82
及结构位移数据，采用三维图形渲染算法中的纹理
80

映射技术，实现对结构表面连续变形过程的可视重 ABAQUS
60 本文方法
建，如图 8 所示。虚拟环境中使结构的形变响应能 40 3D-DIC
够以实物细节呈现，并具有真实的物理特性。该可 20
视化系统完整地再现了结构变形过程，以及双目相 Z / mm 0
机监测系统的布置。其中包括相机/镜头的选择，相 −20
机位置/方向，结构真实变形过程的渲染，以及两者 −40
位置相对关系，完全实现视觉传感器测量结构三维 −60
形变的可视化，通过张正友棋盘标定法 [12] 进行标定， −80
0 0.5 1.0 1.5 2.0 2.5 3.0
重投影误差小于 0.5 pixel，符合应用精度要求。同时 Time / s

在理想仿真环境下对 SVR 的参数进行优化，并可应 图 9 B 点位移时程
用于现场试验中。在标准光强下，随着拟合步长的 Fig. 9 Displacement time-history of point B