Page 31 - 《振动工程学报》2025年第9期

第 9 期 邹云峰，等：采用多级模态组响应重构的密集模态损伤识别方法 1961

0.002 言，单元层面的损伤识别结果均令人满意。

0 相较传统的基于模态应变能的方法，本文所提
等效损伤 −0.002 出的方法不仅扩展了损伤识别在密集模态下的适用
−0.004
−0.006 性， 而 且 能 在 保 证 精 度 的 前 提 下 大 幅 提 升 计 算 效
−0.008 率。接下来将通过多级识别策略和模型缩聚说明该
1 2 3 4 5 6 7 8 9 10 方法在识别效率上的优越性。
超单元序号
(a) DS1 (4次迭代) 首先，对 DS1 和 DS2 考虑不划分子结构分级识
(a) Damage scenario 1 (4 iterations)
别而直接根据式 (9) 搜索桁架左跨的所有单元（搜索
0.004 结构一半的单元足以突出对比性）。设定与 2.3 节相
0 同的初始条件，损伤识别结果如图 11 所示。从图中
等效损伤 −0.004 可以看出，尽管预设损伤的单元仍然有明显的负值，
−0.008
−0.012
−0.016 但两种损伤场景下的其他单元被识别出多处不可忽
略的错误，这会导致损伤的误判，并且整体识别结果
1 2 3 4 5 6 7 8 9 10 的稀疏性也明显下降了。此外，无分级和无模型缩
超单元序号
(b) DS2 (4次迭代) 聚下的损伤识别耗时如表 5 所示。为了增强对比性，
(b) Damage scenario 2 (4 iterations)
无分级识别中使用了缩聚模型，无缩聚模型的情况
0.02
0.01 下则考虑了多级识别。显然，多级识别的应用对效
率有明显的提升，通过分层次的识别减小搜索维度
0
等效损伤 −0.01 可以避免在大多数单元上做无用功。模型缩聚方法
−0.02
−0.03 本身虽然进一步减少了迭代的时间消耗，但由于本
−0.04 案例所选用的桁架结构的矩阵维度仅从 236×236 缩
1 2 3 4 5 6 7 8 9 10
超单元序号 减至 90×90，因此模型缩聚带来的性能提升有限。

(c) DS3(5次迭代)
(c) Damage scenario 3 (5 iterations)
0.02 3 试 验 案 例
0.01
0
等效损伤 −0.01 法的可行性，试验装置如图 12 所示。其中，下部的
通过一个栏杆-平板结构进一步验证损伤识别方
−0.02
−0.03
−0.04 板部件有效长度为 1 m，宽度为 0.32 m；上部的栏杆
−0.05
1 2 3 4 5 6 7 8 9 10 部 件 的 立 柱 高 度为 0.32 m， 并 在 立 柱 高 度 0.1、 0.2
超单元序号
和 0.3 m 处各设置一根长 0.6 m 的横梁，其中 0.1 m 处
(d) DS4(4次迭代)
(d) Damage scenario 4 (4 iterations) 的横梁截面尺寸为 2 cm×2 cm，其余两根横梁的截面

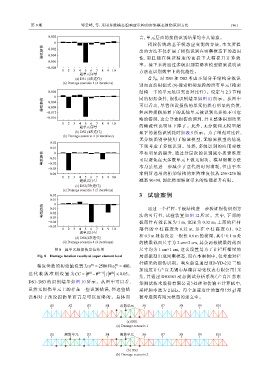
图 8 超单元级损伤定位结果 尺寸均为 1 cm×1 cm，这么设置是为了让栏杆横梁的
Fig. 8 Damage location results at super element level 局部振型出现密集模态，而在本案例中，仅考虑对栏
杆横梁的损伤识别。响应信息通过 HD-YD-232 三轴
精度参数的初始值设置为 η = 2500和 α = 400，
(0)
(0)
s
加速度计（产自无锡市厚德自动化仪表有限公司）采
迭 代 收 敛 准 则 设 置 为 CC = θ −θ (k−1) (k)
/θ ⩽ 0.05。
(k)
集，并通过 DH8303 动态测试分析系统（产自江苏东
DS1~DS3 的识别结果如图 10 所示。从图中可以看， 华测试技术股份有限公司）处理和传输至计算机中，
虽然无损伤单元上的存在一些识别错误，但这些错 采样频率选为 2 kHz。每个加速度计的重量（55 g）都
误相对于预设损伤量而言是可以忽略的。总体而 被考虑到有限元模型的建立中。

S1 S2 S3 S4 离散单元 S6 S7 S8 S9 S10
(a) DS1
(a) Damage scenario 1
S1 离散单元 S3 S4 离散单元 S6 S7 S8 S9 S10

(b) DS2
(b) Damage scenario 2

S1 S2 S3 S4 离散单元 S6 S7 S8 S9 S10

离散单元 离散单元