Page 30 - 《振动工程学报》2025年第9期

1960 振 动 工 程 学 报 第 38 卷

实际响应 重构响应 架中预测等效损伤因子。为了说明模态组响应应变

−4
×10
模态组加速度 / (m·s −2 ) −2 2 0 DS1 下（E57 的 10% 刚度折减）迭代初始阶段前两个
4
能作为损伤敏感特性的可行性，在图
中给出了在
7
模态组响应对等效损伤因子的灵敏度（即偏导数），考
虑到某一单元的应变能对该单元的损伤敏感性远大

−4
˜
r,c

1g
0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 于其他子结构，图 7 的横坐标分别为 mean∂F /∂ ˜ θ 1 , ···,

˜
，
r,c
时间 / s mean∂F /∂ ˜ θ 10 即对应于 10 个超单元的模态组响

(a) 模态组Ⅰ 10g
(a) Modal groupⅠ 应应变能对相应超单元的平均灵敏度绝对值，这里
−3
×10
模态组加速度 / (m·s −2 ) −0.5 0 均值，并且每一个灵敏度关于模态组的最大灵敏度
表示对
t c ×t c 的灵敏度矩阵内的所有元素求
的
mean
1.0
0.5
可以看出，前两个模态组中灵敏度
归一化。从图
7
最大值均出现在预设了损伤的第
个超单元，这说
5
−1.0

0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 明预设损伤能引起模态组响应应变能的明显变化。

时间 / s 1.0
(b) 模态组Ⅱ 0.8
(b) Modal groupⅡ 灵敏度 0.6
−4
×10
模态组加速度 / (m·s −2 ) −2 2 0 0.2 0 1 2 3 4 超单元序号 7 8 9 10
4
0.4
5
6
(a) MG1
−4
0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 (a) The first modal group
时间 / s 1.0
(c) 模态组Ⅲ 0.8
(c) Modal groupⅢ 灵敏度 0.6
−3
×10
模态组加速度 / (m·s −2 ) −1.5 0 0.2 0 1 2 3 4 超单元序号 7 8 9 10
3.0
0.4
1.5
6
5
(b) MG2
−3.0
0.5 1.0 1.5 2.0 2.5 3.0 (b) The second modal group
时间 / s 图 7 模态组响应应变能灵敏度
(d) 模态组Ⅳ Fig. 7 Sensitivity of modal group response strain energy

(d) Modal groupⅣ 纵坐标为超单元等效损伤因子的识别值，根据式 (4)
超单元级的损伤定位结果如图
所示。其中，
8
−4
×10
模态组加速度 / (m·s −2 ) −2.5 0 可知，等效损伤表现为超单元刚度矩阵的整体折减
5.0
2.5
并未标注单位。类似
率，因此是无量纲参数，在图
8
地，后续单元级损伤识别所涉及损伤因子也是无量
−5.0
0.5 1.0 1.5 2.0 2.5 3.0 纲参数。可以看出各损伤场景下的第一级识别均提
时间 / s 供了具有稀疏特性的可疑损伤超单元，第二级损伤
(e) 模态组Ⅴ
(e) Modal groupⅤ 识别在此基础上展开。

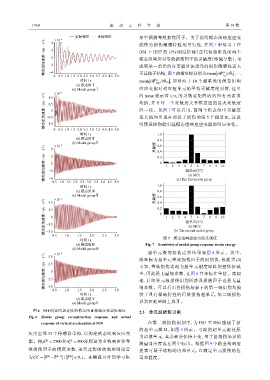
图 6 N10 的竖向加速度的模态组重构响应和实际响应 2.3 单元级损伤识别
Fig. 6 Modal group reconstruction response and actual
response of vertical acceleration at N10 在第二级损伤识别中，为 DS1 至 DS4 重建了新
的超单元模型，如图 9 所示。可疑的超单元被还原
应由全部 33 个传感器重构，以构建模态组响应应变
为离散单元，其余部分保持不变，用于各损伤场景的
能。将 ˜ µ = 2500和 ˜ α = 400分别设为重构响应和等 测量自由度也在图中标出。根据图 9 中的重构响应
(0)
(0)
s
效损伤因子的精度参数，迭代过程的收敛准则设置 搜索可疑子结构的内部单元，以确定单元损伤的位

/˜ θ ⩽ 0.1。在稀疏贝叶斯学习框
为 CC = ˜ θ − ˜ θ (k−1) (k) 置和程度。
(k)