Page 34 - 《振动工程学报》2025年第9期

1964 振 动 工 程 学 报 第 38 卷

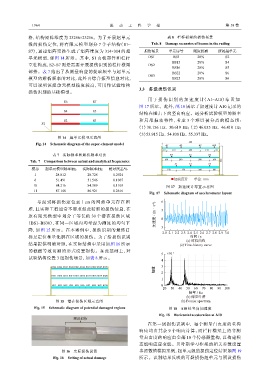
格，结构矩阵维度为 23256×23256。为了开展超单元 表 8 栏杆横梁的损伤场景
级的损伤定位，将有限元模型划分 7 个子结构（S1~ Tab. 8 Damage scenarios of beams in the railing

S7），通过矩阵变换生成了矩阵维度为 314×314 的超 损伤场景 单元序号 刚度折减 所属超单元
单元模型，如图 14 所示。其中，S1 由板部件和栏杆 DS1 BS3 20% S2
BS15 20% S4
立柱构成，S2~S7 则是需要开展损伤识别的栏杆横梁 DS2
BS16 20% S5
部件。表 7 给出了从测量响应的提取频率与超单元 BS22 20% S6
DS3
模型的解析频率的对比，此外再综合振型信息对比， BS25 20% S6
可以说明该超单元模型精度较高，可用作试验结构
3.3 多级损伤识别
损伤识别的基础模型。
用 于 损 伤 识 别 的 加 速 度 计（ A1~A10） 布 置 如

S6 S7
图 17 所示。此外，图 18 展示了加速度计 A10 记录的
S4 S5
结构在锤击下的竖向响应。通分析试验模型的频率
S2 S3 和 局 部 振 动 特 性， 考 虑 3 个 难 以 被 分 离 的 模 态 组 ：
S1
（1） 30.156 Hz、 30.619 Hz； （ 2） 46.055 Hz、 46.410 Hz；
（3）53.915 Hz、54.838 Hz、55.337 Hz。

图 14 超单元模型示意图

Fig. 14 Schematic diagram of the super-element model 600
A7 A8 A9 A10

50 150 200 150 50
表 7 实际频率和解析频率对比 A4 A5 A6
100 200 200 100
Tab. 7 Comparison between actual and analytical frequencies 300
A1 A2 A3
模态 超单元模型频率/Hz 实际频率/Hz 相对误差/% 150 150 200 100
1 28.812 28.728 0.2924
6 51.491 51.546 0.1067 加速度计 单位: mm

10 84.216 84.309 0.1103 图 17 加速度计布置示意图
11 87.148 86.921 0.2616
Fig. 17 Schematic diagram of accelerometer layout

考虑到将损伤定位至 1 cm 的网格单元存在困 6
难，且实际工程通常不要求如此精细的损伤信息，在 3
原有限元模型中划分了等长的 30 个潜在损伤区域 加速度 / (m·s −2 ) 0
（BS1~BS30），在同一区域内均考虑为刚度的均匀下
降，如图 15 所示。在本案例中，损伤识别的最终目 −3
2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0
标是定位和量化潜在区域的损伤。为了给损伤识别 时间 / s
(a) 时程曲线
结果提供明确对照，在实际结构中采用如图 16 所示 (a) Time-history curve
的截面等效切割的形式设置损伤。在此基础上，对 −1
5 ×10
试验结构设置 3 组损伤场景，如表 8 所示。
4

3
幅值 2
BS21 BS22 BS23 BS24 BS25 BS26 BS27 BS28 BS29 BS30
BS11 BS12 BS13 BS14 BS15 BS16 BS17 BS18 BS19 BS20
1
BS1 BS2 BS3 BS4 BS5 BS6 BS7 BS8 BS9 BS10 0
20 30 40 50 60 70 80 90 100
频率 / Hz
(b) 傅里叶谱

图 15 潜在损伤区域示意图 (b) Fourier spectrum

Fig. 15 Schematic diagram of potential damaged regions 图 18 A10 处竖向加速度

Fig. 18 Horizontal acceleration at A10

预设损伤
在第一级损伤识别中， 每个测量自由度的重构
响应均由其余 9 个响应计算，而栏杆横梁上的非测
量自由度的响应由全部 10 个传感器重构，以构建模
态组响应应变能。贝叶斯学习框架的相关参数设置

图 16 实际损伤设置 参照数值模拟案例，超单元级的损伤定位结果如图 19
Fig. 16 Setting of actual damage 所示。识别结果反映的可疑损伤超单元与预设损伤