Page 35 - 《振动工程学报》2025年第9期

第 9 期 邹云峰，等：采用多级模态组响应重构的密集模态损伤识别方法 1965

相对应，且非损伤超单元具备较好的稀疏性，一些错 识别值 预设值
误的负识别值可被忽略。接下来，将在超单元级损 0.05
0
伤定位的基础上进一步开展第二级损伤识别。 −0.05
损伤 −0.10
0.01
0 −0.15
−0.20
−0.01
等效损伤 −0.02 −0.25 BS1 BS2 BS3 BS4 BS5
−0.03
损伤区域序号
−0.04
−0.05 (a) DS1(4次迭代)
−0.06 (a) Damage scenario 1 (4 iterations)
2 3 4 5 6 7
超单元序号 0.05
(a) DS1(5次迭代) 0
(a) Damage scenario 1 (5 iterations) −0.05
0.01 损伤 −0.10
0 −0.15
−0.20
−0.01
等效损伤 −0.02 −0.25 BS11 BS12 BS13 BS14 BS15 BS16 BS17 BS18 BS19 BS20
−0.03
−0.04
−0.05 损伤区域序号
−0.06 (b) DS2(7次迭代)
2 3 4 5 6 7 (b) Damage scenario 2 (7 iterations)
超单元序号
(b) DS2(6次迭代) 0.05
(b) Damage scenario 2 (6 iterations)
0
0.02 −0.05
0 损伤 −0.10
−0.02 −0.15
等效损伤 −0.04 −0.20
−0.06
−0.25
−0.08
BS23
BS24
−0.10 BS21 BS22 损伤区域序号 BS25
−0.12 (c) DS3(5次迭代)
2 3 4 5 6 7 (c) Damage scenario 3 (5 iterations)
超单元序号
(c) DS3(6次迭代) 图 20 第二级损伤识别结果
(c) Damage scenario 3 (6 iterations)
Fig. 20 Damage identification results at the second level

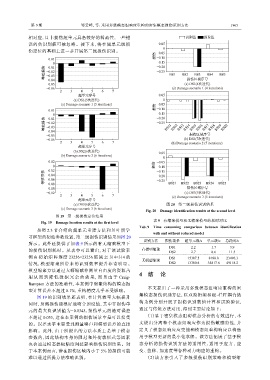
图 19 第一级损伤定位结果

表 9 有缩聚模型和无缩聚模型的耗时对比
Fig. 19 Damage location results at the first level

Tab. 9 Time consuming comparison between identification
参照 2.3 节介绍的超单元重建方法和贝叶斯学
with and without reduced model
习框架的初始参数设置，第二级损伤识别结果如图 20
识别方法 损伤场景 超单元级/s 单元级/s 总耗时/s
所示。此外还提供了如表 9 所示的有无缩聚模型下
DS1 2.2 1.7 3.9
的损伤识别耗时。从表中可以看出，对于该试验案 有模型缩聚 DS2 2.7 8.6 11.3
例 由 初 始 矩 阵 维度 23256×23256 缩 减 至 314×314 的 DS1 15307.5 8188.8 23496.3
无模型缩聚
情况，模型缩聚所带来的识别效率提升非常明显。 DS2 13300.6 35817.6 49118.2
模型缩聚方法通过大幅缩减非测量自由度的资源占
用 从 而 到 降 低 数 据 冗 余 的 效 果， 而 且 由 于 Craig- 4 结 论
Bampton 方法的准确性，本案例中缩聚结构的模态振
本文提出了一种采用多级模态组响应重构的密
型计算误差不超过 0.1%，重构精度几乎不受影响。
集模态损伤识别方法，以双跨桁架和板-栏杆耦合结
图 19 的识别结果还表明，在计算效率大幅提升
构为例分别开展了损伤识别数值计算和试验验证，
同时，预测损伤能很好地吻合预设值，其中非损伤单
元的最大负识别值为−0.0343，损伤单元的绝对误差 通过与传统方法对比，得到主要结论如下：
不超过 0.035，这在本案例的损伤场景中是可以接受 （1）鉴于密集模态阻碍模态分析的有效进行，本
的。误差水平主要受到测量噪声和模型误差的直接 文提出分离整个模态组响应作为损伤敏感特性，并
影响。此外，由于所提出的方法本质上是基于模态 定义了模态组响应应变能和模态组重构响应以构造
参数的，因此结构本身的阻尼和外荷载形式等因素 用于模型更新的最小化求解。该方法拓展了基于模
也会通过模态提取精度间接影响损伤识别结果。对 态分析的损伤识别方法的适用性，适用于应力、应
于本案例而言，潜在损伤区域内小于 5% 的损伤可能 变、位移、加速度等各种动力响应的重构。
难以通过所提方法准确识别。 （2）该方法引入了多级损伤识别策略和模型缩