Page 162 - 《振动工程学报》2025年第9期

2092 振 动 工 程 学 报 第 38 卷

2 倍的第 2 阶正向模态频率。每一个交叉点都意味 2.3 非同步接触运动的时域与频域特征
着可能有正反向模态频率 2∶1 的内共振。当转速 Ω≈
为了分析非同步响应的时域与频域特征，对上
291.7 r/min 时，对应第 1 阶反向模态频率等于 3 倍的
述仿真得到的水平位移的时域信号进行功率谱密度
第 1 阶正向模态频率；当转速 Ω≈344.5 r/min 时，对应
分析，如图 5 所示，从图中可以看出，在两个非同步
第 2 阶反向模态频率等于 3 倍的第 1 阶正向模态频
共振转频区间内，频率成分包括转频、两个非同步
率；当转速 Ω≈430.2 r/min，对应第 1 阶反向模态频率
频率成分，该非同步频率成分分别对应于转子的正
等于 3 倍的第 2 阶正向模态频率；当转速 Ω≈482.9 r/min
向和反向涡动频率。为了清晰地分析该非同步频率
时，对应第 2 阶反向模态频率等于 3 倍的第 2 阶正向
成分，提取特定转速下的响应进行频率分析。
模态频率。每一个交叉点都意味着可能有正反向模

态频率 3∶1 的内共振。 20

18
−50
2.2 非线性响应随转速变化的规律 16
14
−100
为了准确验证正反向模态频率重合处得到的内 Ω / Hz 12 幅值 / dB
10
共振对应转速，采用 4 阶 Runge-Kutta 法求解运动方 ^ 8 −150
程 (10)，判断初始的转子状态是否与静子接触，如果 6 −200
4
转静子未接触，则采用无接触情况下的转子线性系 −250
2
统进行求解，采用事件检测函数检测转静子接触，其 0
0 5 10 15 20
终了状态作为转静子接触的初始状态，建立接触后 频率成分 / Hz

产生的激振力，求解转静子接触情况下的转子响应， 图 5 功率谱密度图
直至采用事件检测函数检测到转静子未接触，通过 Fig. 5 Power spectral density plot

此方法循环计算，得到系统的稳态响应。这里的事
2.3.1 3∶1 内共振
件检测函数在常微分方程 ODE 的求解过程中，能精
在非同步接触转速区间 [384，486] r/min，即图 5
确检测到转静子接触时刻，提示常微分方程 ODE 求
所示的转频区间 [6.4，8.1] Hz 内，选取转速 411 r/min，
解器停止积分。
初始状态为在 x 轴上对转子 2 施加 10 rad 的角向位
−3
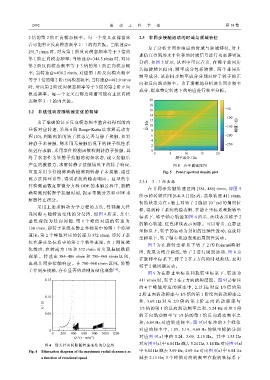
采用上述求解动力学方程的方法，得到最大径
移，得到转子系统的稳态解，在静止坐标系和旋转坐
向间隙 r 2 随转速变化的分岔图，如图 4 所示，其中，
标系下，转子轴心轨迹如图 6 所示，蓝线表示转子 2
蓝 色 虚 线 为 径 向 间 隙， 第 1 个 峰 值 对 应 的 转 速 为
的轴心轨迹，红色虚线表示间隙。可以看出，在静止
138 r/min，即转子系统在静止坐标系中的第 1 个临界
坐标系下，转子的运动为封闭的连续性进动；在旋转
速度；第 2 个峰值对应的转速为 372 r/min，即转子系
坐标系下，转子轴心轨迹表现出周期性运动。
统在静止坐标系中的第 2 个临界速度，由于刚度硬
图 7 为 在 旋 转 坐 标 系 下 转 子 2 的 Poincaré映 射
化效应，在转速为 138 和 372 r/min 时出现振幅跳跃
图，表现为闭合曲线，转子 2 进行周期运动，图 8 为
现 象 。 转 速在 384~486 r/min 和 780~960 r/min 区 间 ，
在旋转坐标系下，转子 2 在 x 方向的时域曲线，表明
出现非同步接触响应。在 780~960 r/min 区间，转静
转子 2 做周期运动。
子非同步接触，存在显著的动刚度硬化现象 [19] 。
图 9 为在静止坐标系和旋转坐标系下，转速为

0.15 411 r/min 时，转子 2 在 x 方向的频谱图。图 9（a）标注

的 4 个峰值对应的频率中，2.15 Hz 对应 1/3 倍的第
0.10 2 阶正向涡动频率与 1/3 倍的第 1 阶反向涡动频率之
和， 3.69 Hz 对 应 2/3 倍 的 第 2 阶 正 向 涡 动 频 率 与
r 2 / m 1/3 倍的第 1 阶反向涡动频率之和，5.24 Hz 对应 1 倍

0.05
的正向涡动频率与 1/3 倍的第 1 阶反向涡动频率之
和，6.84 Hz 对应转速频率；图 9（b）标注的 3 个峰值
对应的频率中，1.55、3.14、4.69 Hz 的纵坐标值分别
0
0 200 400 600 800 1000 1200
−1
Ω / (r·min ) 对 应图 9（ a） 中 的 5.24、 3.69、 2.15 Hz。 其 中 1.55 Hz

对应图 9（a）中 6.84 Hz 减去 5.24 Hz，3.14 Hz 对应图 9（a）
图 4 最大径向间隙随转速变化的分岔图
中 6.84 Hz 减去 3.69 Hz，4.69 Hz 对应图 9（a）中
Fig. 4 Bifurcation diagram of the maximum radial clearance as 6.84 Hz
a function of rotational speed 减去 2.15 Hz；3 个峰值对应的频率在旋转坐标系下