Page 161 - 《振动工程学报》2025年第9期

第 9 期 王海飞，等：柔性转静子碰撞正反向模态内共振特性研究 2091

表 1 计算参数
20
Tab. 1 Calculation parameters 18

16
参数 数值
14
圆盘1的直径 d 1 /mm 46
10
圆盘2的直径 d 2 /mm 46 ω / Hz 12
圆盘1的厚度 v 1 /mm 19 8
6
圆盘2的厚度 v 2 /mm 19 4
圆盘1的质量 M 1 /kg 0.28 2
0
圆盘2的质量 M 2 /kg 0.42 0 200 400 600 800 1000 1200
−1
Ω / (r·min )
圆盘1的偏心量 ε 1 /mm 2
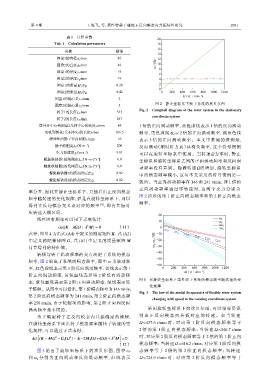
图 2 静止坐标系下转子系统的坎贝尔图
圆盘2的偏心量 ε 2 /mm 3
转子1的长度 L 1 /mm 333 Fig. 2 Campbell diagram of the rotor system in the stationary
coordinate system
转子2的长度 L 2 /mm 257
缓冲环中心到圆盘2几何中心的长度 a/mm 84 1 倍的正向涡动频率，蓝色虚线表示 1 倍的反向涡动
电机到圆盘1几何中心的长度 b/mm 166.5 频率，黑色虚线表示 2 倍的正向涡动频率，淡蓝色线
缓冲环的静子径向间隙 c/mm 10 表示 3 倍的正向涡动频率。本文中常用的惯例是，
−1
静子的刚度 k s /(N·m ) 200 反向涡动（顺时针方向）具有负频率，这个符号惯例
重力加速度 g/(m·s ) 9.81 可以在旋转坐标系中使用。当转速 Ω为零时，静止
−2
−1
螺旋联轴器1的角刚度 k r1 /[N·m·(°) ] 6.0 坐标系和旋转坐标系之间的正向涡动频率和反向涡
螺旋联轴器2的角刚度 k r2 /[N·m·(°) ] 6.0 动频率没有差别。随着转速 Ω的增加，旋转坐标系
−1
螺旋联轴器1的模态阻尼比 ζ 1 0.02 中的模态频率减小，这与本文采用的符号惯例是一
螺旋联轴器2的模态阻尼比 0.02
致的。当正向涡动频率在 146 和 241 r/min，即 1 倍的
ζ 2
正 向 涡 动 频 率 通 过 零 转 速 时， 这 两 个 交 点 分 别 为
率分开，因此在静止坐标系下，只能看出正反向模态
图 2 所示的第 1 阶正向模态频率和第 2 阶正向模态
频率随转速的变化规律，但是在旋转坐标系下，可以
频率。
得到正反向模态交叉点对应的频率 [16] ，即内共振对

应转速大概区间。
20
线性固有频率可以用下式来估计： 10 ω f
ω b
2
det(K −λGΩ+λ M) = 0 （11） 0 2ω f
3ω f
式中，向量 λ 为由式 (A4) 中定义的刚度矩阵 K、式 (A2) −10
中定义的陀螺矩阵 G、式 (A1) 中定义的质量矩阵 M ω f , ω b / Hz −20
计算得到的特征值。 −30
−40
转频与转子涡动频率的交点决定了系统的模态
−50
频率，图 2 给出了系统的模态频率，图中 ω 为涡动频
−60
率，红色虚线表示第 1 阶反向涡动频率，蓝线表示第 1 0 200 400 600 800 1000 1200
−1
Ω / (r·min )
阶正向涡动频率，黄色虚线表示第 2 阶反向涡动频
图 3 在旋转坐标系下柔性转子系统的模态频率随转速的变
率，紫色虚线表示第 2 阶正向涡动频率，绿线表示转
化规律
子转频。从图中可以看出，第 1 阶模态频率为 146 r/min，
Fig. 3 The law of the modal frequencies of flexible rotor system
第 2 阶反向模态频率为 241 r/min，第 2 阶正向模态频
changing with speed in the rotating coordinate system
率 250 r/min，由于陀螺项的影响，第 2 阶正向和反向
涡动频率是不同的。 采用旋转坐标系下的坎贝尔图，可以很容易识
为了确定转子正反向模态内共振确定的转频， 别 出 正 反 向 模 态 内 共 振 对 应 的 转 速 。 如 当 转 速
在旋转坐标系下画出转子模态频率随转子转速的变 Ω≈437.6 r/min 时 ， 对 应 第 1 阶 反 向 模 态 频 率 等 于
化规律，可以通过下式求得： 2 倍 的 第 1 阶 正 向 模 态 频 率 ； 当 转 速 Ω≈546.7 r/min
[ ] 时，对应第 2 阶反向模态频率等于 2 倍的第 1 阶正向
2
2
2
det (K − MΩ −GJΩ )−λ(−2MJΩ+GΩ)+λ M = 0
（12） 模态频率；当转速 Ω≈616.2 r/min，对应第 1 阶反向模
图 3 给出了旋转坐标系下的坎贝尔图，图中 ω f 态 频 率 等于 2 倍 的 第 2 阶 正 向 模 态 频 率 ； 当 转 速
和 ω b 分 别 为 正 向 涡 动 和 反 向 涡 动 频 率 ， 红 线 表 示 Ω≈724.9 r/min 时 ， 对 应 第 2 阶 反 向 模 态 频 率 等 于