Page 159 - 《爆炸与冲击》2025年第12期
P. 159
第 45 卷 刘振华,等: 基于非常规态近场动力学对混凝土动态拉伸断裂的数值模拟研究 第 12 期
PD 作为非局部理论,其中粒子间距 Δx 和邻域半径 δ 均会对模拟结果产生影响,为准确预测一维杆
中的弹性波传播首先进行收敛性分析 [38] ,即 δ 收敛性和 m= δ/Δx 收敛性。其中 δ 收敛性通过固定 m=3.0,
改变 δ(0.001 2、0.003 和 0.006 m)取值研究其收敛性;m 收敛性通过固定 δ=0.001 2 m,改变 m(1.5、3.0 和
6.0)取值研究其收敛性。此外,采用均匀离散方式,时间步长根据最小粒子间距下(Δx=0.000 2 m)的稳定
时间步长确定。
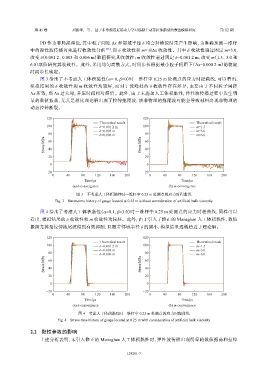
图 3 给出了不考虑人工体积黏性(α= 0,β=0)时一维杆中 0.25 m 处测点的应力时程曲线,可以看出,
模拟结果的 δ 收敛性和 m 收敛性均较好,而对于波峰处的 δ 收敛性存在差异,主要由于不同粒子间距
Δx 所致,当 Δx 过大时,升压时间相对滞后。此外,由于未施加人工体积黏性,弹性波传播过程中发生明
显的数值振荡,尤其是相比理论解出现了拉伸拖尾波,该非物理的拖尾波可能会导致材料出现非物理的
动态拉伸断裂。
120 120
Theoretical result Theoretical result
100 δ=0.001 2 m 100 m=1.5
δ=0.003 m m=3.0
80 δ=0.006 m 80 m=6.0
Stress/MPa 60 Stress/MPa 60
40
40
20 20
0 0
−20 −20
0 40 80 120 160 200 0 40 80 120 160 200
Time/μs Time/μs
(a) δ-convergence (b) m-convergence
图 3 不考虑人工体积黏性时一维杆中 0.25 m 处测点的应力时程曲线
Fig. 3 Stress-time history of gauge located at 0.25 m without consideration of artificial bulk viscosity
图 4 给出了考虑人工体积黏性(α=0.1,β=3.0)时一维杆中 0.25 m 处测点的应力时程曲线,同样可以
看出,模拟结果的 δ 收敛性和 m 收敛性均较好。此外,由于引入了修正的 Monaghan 人工体积黏性,数值
振荡尤其是拉伸拖尾波得到有效抑制,且随着邻域半径 δ 的减小,模拟结果逐渐趋近于理论解。
120 120
Theoretical result Theoretical result
100 δ=0.001 2 m 100 m=1.5
δ=0.003 m m=3.0
80 δ=0.006 m 80 m=6.0
Stress/MPa 60 Stress/MPa 60
40
40
20 20
0 0
−20 −20
0 40 80 120 160 200 0 40 80 120 160 200
Time/μs Time/μs
(a) δ-convergence (b) m-convergence
图 4 考虑人工体积黏性时一维杆中 0.25 m 处测点的应力时程曲线
Fig. 4 Stress-time history of gauge located at 0.25 m with consideration of artificial bulk viscosity
2.2 黏性参数的影响
上述分析表明,未引入修正的 Monaghan 人工体积黏性时,弹性波传播出现明显的数值振荡和拉伸
124201-7