Page 163 - 《爆炸与冲击》2025年第12期
P. 163
第 45 卷 刘振华,等: 基于非常规态近场动力学对混凝土动态拉伸断裂的数值模拟研究 第 12 期
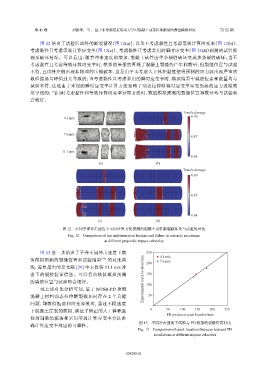
图 12 给出了试验后试件的断裂情况(图 12(a)),以及不考虑黏性且考虑等效计算应变率(图 12(b))、
考虑黏性且考虑等效计算应变率(图 12(c))、考虑黏性且考虑常用的瞬时应变率(图 12(d))预测的试件断
裂及破坏情况。可以看出:随着冲击速度的增加,混凝土试件由单条裂缝破坏变成多条裂缝破坏;当不
考虑黏性且考虑等效计算应变率时,模拟结果虽然再现了混凝土裂缝的产生和数量,但裂缝位置与试验
不符,且试件左侧出现非物理的压缩破坏,这是由于未考虑人工体积黏性使得预测的应力波出现严重的
数值振荡且峰值过大导致的;当考虑黏性且考虑常用的瞬时应变率时,模拟结果中裂缝位置和数量均与
试验不符,这是由于常用的瞬时应变率计算方法忽略了动态拉伸断裂时应变率突变引起的应力迟滞效
应导致的;当同时考虑黏性和等效计算应变率计算方法时,数值模拟预测的裂缝位置和数量均与试验吻
合较好。
Tensile damage
4.1 m/s 0.90
7.6 m/s
0.87
11.1 m/s
0.84
(a) (b)
Tensile damage
0.90
0.87
0.84
(c) (d)
图 12 不同子弹冲击速度下不同计算方法预测的混凝土试件断裂破坏及与试验的对比
Fig. 12 Comparison of test and numerical fracture and failure in concrete specimens
at different projectile impact velocities
图 13 进一步给出了子弹不同冲击速度下数 250
值模拟预测的裂缝位置和试验结果 [39] 的对比曲 200 4.1 m/s
7.6 m/s
线,需要指出的是文献 [39] 中未提供 11.1 m/s 冲
击下的裂缝位置信息。可以看出数值模拟预测 150
的裂缝位置与试验吻合很好。 Experimental crack location/mm 100
经上述对比分析可知,基于 NOSB-PD 预测
混凝土材料动态拉伸断裂破坏时存在 2 个关键 50
问题,即数值振荡和应变率效应,通过不同速度
下混凝土层裂的模拟,验证了修正的人工体积黏 0 50 100 150 200 250
PD predicted crack location/mm
性抑制数值振荡和采用等效计算应变率方法准
图 13 不同冲击速度下试验与 PD 模拟的裂缝位置对比
确计算应变率效应的可靠性。
Fig. 13 Comparison of crack locations between test and PD
simulations at different impact velocities
124201-11