Page 59 - 《软件学报》2020年第12期

王丽萍 等:偏好向量引导的高维目标协同进化算法 3725

测试问题:WFG2 测试问题:WFG3 测试问题:WFG4
0.50 0.30
0.45
0.45
指标值 0.40 指标值 0.40 指标值 0.25

HV 0.35 HV 0.35 HV 0.20
0.30
0.30 0.15
0.25
0.5 1 1.5 2 4 0.5 1 1.5 2 4 0.5 1 1.5 2 4

β β β
(a) WFG2 (b) WFG3 (c) WFG4

测试问题:WFG5 测试问题:WFG6 测试问题:WFG7
0.30 0.30
0.30
指标值 0.25 指标值 0.25 指标值

HV 0.20 HV 0.20 HV 0.25

0.15 0.15 0.20
0.5 1 1.5 2 4 0.5 1 1.5 2 4 0.5 1 1.5 2 4

β β β
(d) WFG5 (e) WFG6 (f) WFG7

测试问题:WFG8 测试问题:WFG9
0.30
0.30
指标值 0.25 指标值 0.25

HV 0.20 HV 0.20

0.5 1 1.5 2 4 0.5 1 1.5 2 4

β β
(g) WFG8 (h) WFG9
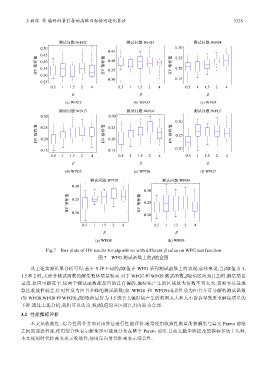
Fig.7 Box plots of HV results for algorithms with different β value on WFG test function
图 7 WFG 测试函数上的β值盒图
从上述实验结果分析可得:基于 5 种不同的β取值在 WFG 系列测试函数上的表现,总体来说,当β取值为 1,
1.5 和 2 时,大部分测试函数的解集整体质量较高.对于 WFG7 和 WFG9 测试函数,β取值区间为[1,2]时,解集质量
最高.原因可能在于,这两个测试函数都是凹的且有偏的,偏好集产生的区域放大倍数不宜太大,否则容易造成
算法收敛性较差.针对性质为凹且多峰的测试函数(如 WFG4 和 WFG9)或者性质为凹且不可分解的测试函数
(如 WFG6,WFG8 和 WFG9),β的取值最好为 1.5 或者 2,偏好集产生的范围太大和太小皆会导致所求解集质量的
下降.通过上述分析,我们可以认为,将β取值设在区间[1,2]内较为合理.

3.2 性能指标评价
本文从收敛性、综合性两个方面对该算法进行性能评价.通常使用收敛性衡量所获解集与真实 Pareto 前沿
之间的逼近程度,使用综合性表示解集尽可能地分布在整个 Pareto 前沿.目前文献中所提及的指标多达十几种,
本文使用时代距离来表示收敛性,使用反向时代距离表示综合性.