Page 54 - 《软件学报》2020年第12期

3720 Journal of Software 软件学报 Vol.31, No.12, December 2020

1
F = (4)
g
1 α+
⎧ 1, n = 0
g
α = ⎨ ⎪ n − 1 (5)
g
⎪ , otherwise
⎩ 2N − 1
其中,N 是候选解个数.
根据适应值赋值法的定义可知 ,偏好集的产生范围依赖于两个参数 :上界值 (goalUpper)和下界 值
(goalLower).更通俗来说,种群中最优个体与最差个体的差值,会决定偏好集的范围.如果偏好集只产生在某个
区域,则在此区域内的候选解具有较大可能性被选作父代来产生子代.这主要是由于这些候选解能够支配更多
的偏好集,从而并获得更高的适应值;反之亦然.由此可知,候选解会向该区域内部的 Pareto 前沿逼近.因此,我们
能够通过设定偏好集的上界和下界,引导候选解朝着决策者感兴趣的区域进化.
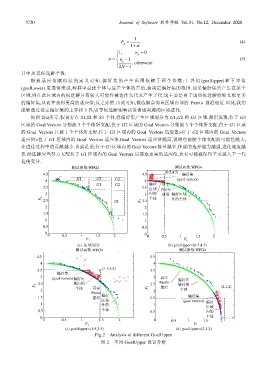
如图 2(a)所示,假设存在 S1,S2 和 S3 个体,将偏好集产生区域划分为 G1,G2 和 G3 区域.我们发现:位于 G3
区域的 Goal Vectors 分别被 3 个个体所支配,位于 G2 区域的 Goal Vectors 分别被 3 个个体所支配,位于 G1 区域
的 Goal Vectors 只被 1 个个体所支配.位于 G3 区域内的 Goal Vectors 适应值>位于 G2 区域内的 Goal Vectors
适应值>位于 G1 区域内的 Goal Vectors 适应值.Goal Vectors 适应值越高,说明它被解个体支配的可能性越大,
在进化过程中的贡献越小.也就是说,位于 G1 区域内的 Goal Vectors 数量越多,种群的选择能力越强,进化速度越
快.候选解应当努力支配位于 G1 区域内的 Goal Vectors 以获取更高的适应值,更有可能被保留下来进入下一代
遗传变异.
测试函数:WFG4 测试函数:WFG4
4.5 4.5 (0.5,4.5) 偏好集
4 S1 G1 G2 G3 4 (gaol vectors)
G1 G2 偏好 真实
3.5 S2 3.5 区域 Pareto
3 3 内的 前沿 偏好区域
F 2 2.5 G1 F 2 2.5 个体 外的个体
2 2
1.5 S3 1.5
1 1
0.5 0.5
0 0
0 0.5 1 1.5 2 0 0.5 1 1.5 2
F 1 F 1
(a) 区域划分 (b) goalUpper=(0.5,4.5)
测试函数:WFG4 测试函数:WFG4
4.5 4.5
4 4
3.5 (1.5,3.5) 3.5
偏好集
3 (gaol vectors) 偏好区 3 真实 偏好区
2.5 域内的 2.5 Pareto 域外的
F 2 个体 真实 F 2 前沿 (2.1,2)
2 2 个体
Pareto
1.5 前沿 偏好 1.5 偏好集
区域 (gaol vectors) 偏好
1 外的 1 区域
0.5 个体 0.5 内的
0 个体
0 0.5 1 1.5 2 0 0.5 1 1.5 2
F 1
F 1
(c) goalUpper=(1.5,3.5) (d) goalUpper=(2,1.2)
Fig.2 Analysis of different GoalUpper
图 2 不同 GoalUpper 设置分析