Page 58 - 《软件学报》2020年第12期

3724 Journal of Software 软件学报 Vol.31, No.12, December 2020

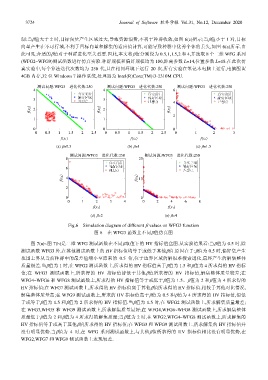
制:当β值大于 2 时,目标向量产生区域过大,导致资源浪费,不利于种群收敛,如图 6(e)所示;当β值小于 1 时,目标
向量产生在不可行域,不利于目标向量和解集的适应值计算,可能导致种群中优秀个体的丢失,如图 6(a)所示.由
此可见,合适的β值对于种群进化至关重要.因此,本文将β值分别设为 0.5,1,1.5,2 和 4,并选取 8 个二维 WFG 系列
(WFG2~WFG9)测试函数进行仿真实验.种群规模和偏好规模均为 100,距离参数 L=14,位置参数 L=18.在此次仿
真实验中,每个算法迭代次数均为 250 代,且在相同环境下运行 20 次.所有实验在笔记本电脑上运行,电脑配置
4GB 内存,32 位 Windows 7 操作系统,处理器为 Intel(R)Core(TM)i3-2310M CPU.

测试问题:WFG3 进化代数:250 测试问题:WFG3 进化代数:250 测试问题:WFG3 进化代数:250
4 4 6
3 3 4
f(x 2) 2 f(x 2) 2 f(x 2)

2
1 1
0 0 0
0 0.5 1 1.5 2 2.5 0 0.5 1 1.5 2 2.5 0 1 2 3

f(x 1) f(x 1) f(x 1)
(a) β=0.5 (b) β=1 (c) β=1.5

测试问题:WFG3 进化代数:250 测试问题:WFG3 进化代数:250
8 20
6
f(x 2) 4 ) f(x 2 10

2
0 0
0 1 2 3 4 0 2 4 6 8
f(x 1) f(x 1)
(d) β=2 (e) β=4
Fig.6 Simulation diagram of different β values on WFG3 function
图 6 在 WFG3 函数上不同β值仿真图
图 7(a)~图 7(h)是二维 WFG 测试函数在不同β取值下的 HV 指标值盒图.从实验结果看:当β值为 0.5 时,除
测试函数 WFG3 外,在其他测试函数上的 HV 指标值均等于或低于其他β值.原因在于:β值为 0.5 时,偏好集产生
范围上界从当前种群中的最差值缩小至原来的 0.5 倍,位于边界区域的解很难搜索进化,最终产生的解集整体
质量很差.当β值为 1 时,在 WFG2 测试函数上,所求得的 HV 指标值高于β值为 1.5 和β值为 4 所求得的 HV 指标
值;在 WFG3 测试函数上,所求得的 HV 指标值皆低于其他β值所求得的 HV 指标值,解集整体质量较差;在
WFG4~WFG6 和 WFG8 测试函数上,所求得的 HV 指标值等于或低于β值为 1.5、β值为 2 和β值为 4 所求得的
HV 指标值;在 WFG7 测试函数上,所求得的 HV 指标值高于其他β值所求得的 HV 指标值,相较于其他对比情况,
解集整体质量高;在 WFG9 测试函数上,所求的 HV 指标值高于β值为 0.5 和β值为 4 所求得的 HV 指标值,但低
于或等于β值为 1.5 和β值为 2 所求得的 HV 指标值.当β值为 1.5 时,在 WFG2 测试函数上,所求解集质量最差;
在 WFG3,WFG5 和 WFG9 测试函数上,所求解集质量最好;在 WFG4,WFG6~WFG8 测试函数上,所求解集整体
质量低于β值为 2 和β值为 4 所求得的解集质量;当β值为 2 时,在 WFG2,WFG4~WFG8 测试函数上,所求解集的
HV 指标值等于或高于其他β值所求得的 HV 指标值;在 WFG3 和 WFG9 测试函数上,所求解集的 HV 指标值并
没有明显优势.当β值为 4 时,在 WFG 系列测试函数上,与其他β值所求得的 HV 指标值相比没有明显优势,在
WFG2,WFG7 和 WFG9 测试函数上表现较差.