Page 62 - 《软件学报》2020年第12期

3728 Journal of Software 软件学报 Vol.31, No.12, December 2020

PICEA-g 在 WFG2-WFG4 测试函数上均优于 g-NSGA-II 和 r-NSGA-II.原因在于:随着目标维数的增加,g-NSGA-
II 和 r-NSGA-II 的选择个体机制是基于 Pareto 占优的,选择能力急剧下降,而协同进化机制能有效克服这一缺
陷,减少目标空间中非支配解得比例,加快种群收敛速度.从指标方差看,3 种算法所求解集质量较稳定.
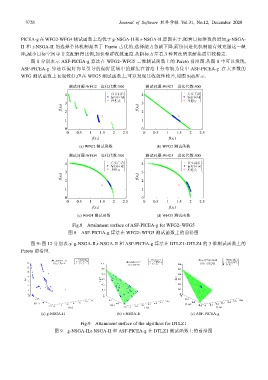
图 8 分别表示 ASF-PICEA-g 算法在 WFG2~WFG5 二维测试函数上的 Pareto 前沿图.从图 8 中可以发现,
ASF-PICEA-g 算法以偏好向量引导的偏好区域中的解集在前沿上分布较为集中.ASF-PICEA-g 在大多数的
WFG 测试函数上表现较好,但在 WEG5 测试函数上,可以发现其收敛性较差,如图 8(d)所示.

测试问题:WFG2 进化代数:500 测试问题:WFG3 进化代数:500

4 4

f(x 2) 3 f(x 2) 3
2 2

1 1
0 0
0 0.5 1 1.5 2 2.5 0 0.5 1 1.5 2 2.5
f(x 1) f(x 1)
(a) WFG2 测试函数 (b) WFG3 测试函数

测试问题:WFG4 进化代数:500 测试问题:WFG5 进化代数:500

4 4

3 3
f(x 2) f(x 2)
2 2
1 1
0 0
0 0.5 1 1.5 2 2.5 0 0.5 1 1.5 2 2.5
f(x 1) f(x 1)
(c) WFG4 测试函数 (d) WFG5 测试函数
Fig.8 Attainment surface of ASF-PICEA-g for WFG2~WFG5
图 8 ASF-PICEA-g 算法在 WFG2~WFG5 测试函数上的前沿图
图 9~图 12 分别表示 g-NSGA-II,r-NSGA-II 和 ASF-PICEA-g 算法在 DTLZ1~DTLZ4 的 3 维测试函数上的
Pareto 前沿图.

(a) g-NSGA-II (b) r-NSGA-II (c) ASF-PICEA-g
Fig.9 Attainment surface of the algrithms for DTLZ1
图 9 g-NSGA-II,r-NSGA-II 和 ASF-PICEA-g 在 DTLZ1 测试函数上的前沿图