Page 63 - 《软件学报》2020年第12期

王丽萍 等:偏好向量引导的高维目标协同进化算法 3729

(a) g-NSGA-II (b) r-NSGA-II (c) ASF-PICEA-g
Fig.10 Attainment surface of the algrithms for DTLZ2
图 10 g-NSGA-II,r-NSGA-II 和 ASF-PICEA-g 在 DTLZ2 测试函数上的前沿图
Pareto前沿
120 测试函数:DTLZ3 求得的解集
参考点
进化代数:500
100
80
60
40
20
0
0
50
100 150
目标1 150 200 50 100
250 0 目标2
(a) g-NSGA-II (b) r-NSGA-II (c) ASF-PICEA-g
Fig.11 Attainment surface of the algrithms for DTLZ3
图 11 g-NSGA-II,r-NSGA-II 和 ASF-PICEA-g 在 DTLZ3 测试函数上的前沿图

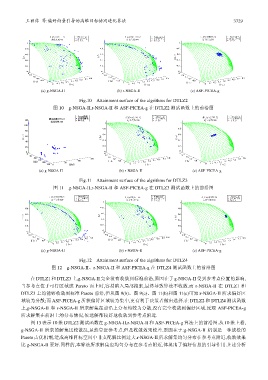
(a) g-NSGA-II (b) r-NSGA-II (c) ASF-PICEA-g
Fig.12 Attainment surface of the algrithms for DTLZ4
图 12 g-NSGA-II、r-NSGA-II 和 ASF-PICEA-g 在 DTLZ4 测试函数上的前沿图

在 DTLZ1 和 DTLZ3 上,g-NSGA-II 完全没有收敛到标准前沿,原因在于 g-NSGA-II 受到参考点位置的影响,
当参考点位于可行区域或 Pareto 面上时,容易陷入局部搜索,最终导致算法不收敛.而 r-NSGA-II 在 DTLZ1 和
DTLZ3 上均能够收敛到标准 Pareto 前沿,但从图 9(b)、图 9(c)、图 11(b)和图 11(c)可知:r-NSGA-II 所求偏好区
域较为分散;而 ASF-PICEA-g 所获偏好区域较为集中,更有利于决策者做出选择.在 DTLZ2 和 DTLZ4 测试函数
上,g-NSGA-II 和 r-NSGA-II 所求解集在前沿上分布均较为分散,没有完全收敛到偏好区域.反观 ASF-PICEA-g
所求解集在前沿上的分布情况,候选解都较好地收敛到参考点附近.
图 13 表示 10 维 DTLZ2 测试函数在 g-NSGA-II,r-NSGA-II 和 ASF-PICEA-g 算法上的前沿图.从 10 维上看,
g-NSGA-II 所求的解集比较散乱,虽然靠近参考点,但是收敛效果较差.原因在于:g-NSGA-II 机制是一种放松的
Pareto 占优机制,造成高维目标空间中非支配解比例过大.r-NSGA-II 所求解集均匀分布在参考点附近,收敛效果
比 g-NSGA-II 要好.同样的,本算法所求解集也均匀分布在参考点附近,体现出了偏好信息的引导作用.上述分析