Page 56 - 《软件学报》2020年第12期

3722 Journal of Software 软件学报 Vol.31, No.12, December 2020

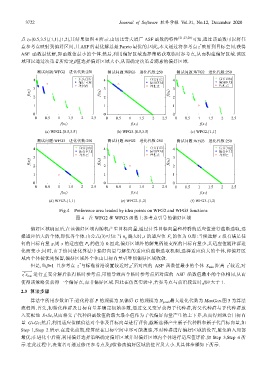
点 z=[0.5,3.5],[1,1],[1,2],其结果如图 4 所示.由切比雪夫增广 ASF 函数的特性 [21,27,28] 可知,通过该函数可以将任
*
意参考点映射到偏好区间,且 ASF 的最优解总是 Pareto 最优的.因此,本文通过将参考点 z 映射到目标空间,获得
ASF 函数最优解,即函数值最小的个体.然后,利用偏好区域选择策略获取临时参考点,从而构建偏好区域.该区
域可以通过决策者所给定β值选择偏好区域大小,从而确定决策者满意的偏好区域.

测试问题:WFG2 进化代数:250 测试问题:WFG3 进化代数:250 测试问题:WFG2 进化代数:250

4 4 4

3 3 3
f(x 2) f(x 2) f(x 2)
2 2 2
1 1 1
0 0 0
0 0.5 1 1.5 2 2.5 0 0.5 1 1.5 2 2.5 0 0.5 1 1.5 2 2.5

f(x 1) f(x 1) f(x 1)
(a) WFG2-[0.5,3.5] (b) WFG3-[0.5,3.5] (c) WFG2-[1,1]

测试问题:WFG3 进化代数:250 测试问题:WFG2 进化代数:250 测试问题:WFG3 进化代数:250

4 4 4

f(x 2) 3 f(x 2) 3 f(x 2) 3
2 2 2
1 1 1
0 0 0
0 0.5 1 1.5 2 2.5 0 0.5 1 1.5 2 2.5 0 0.5 1 1.5 2 2.5

f(x 1) f(x 1) f(x 1)
(d) WFG3-[1,1] (e) WFG2-[1,2] (f) WFG3-[1,2]
Fig.4 Preference area leaded by idea points on WFG2 and WFG3 functions
图 4 在 WFG2 和 WFG3 函数上参考点引导的偏好区域

偏好区域确定后,在该偏好区域内随机产生目标向量,通过计算目标向量和种群的适应值进行截断选取,选
择适应值大的个体,即优秀个体.由公式(3)可知:当 n g 越大时,s 的适应值 F s 的值为 0.即:当候选解 s 没有满足任
何的目标向量 g,则 s 的适应值 F s 的值为 0.因此,偏好区域外的解集所能支配的目标向量少,其适应值随种群进
化而变小;同时,由于协同进化算法中偏好向量与解集的适应值截断选取机制,选择适应值大的个体,即偏好区
域内个体被优先保留,偏好区域外个体由目标向量引导朝偏好区域收敛.
*
*
*
但是,当β=1 且参考点 z 与标准前沿设置较近时,z 所对应的 ASF 函数值最小的个体 S min 距离 z 较近,对

*
zs min 进行正交分解后获得临时参考点,可能导致两个临时参考点所对应的 ASF 函数值最小的个体相同,从而
使得该策略仅获得一个偏好点,而非偏好区域.因此在仿真实验中,若参考点与前沿较近时,β应大于 1.
2.3 算法步骤
算法中所用参数如下:进化种群 P 的规模为 N,偏好 G 的规模为 N goal ,最大进化代数为 MaxGen.图 5 为算法
流程图.首先,初始化种群及目标向量并确定初始参数,通过交叉变异获得子代种群,将父代种群与子代种群放
入交配池 S+Sc,从而将父子代种群函数值的最大最小值作为子代偏好向量产生的上下界,从而得到混合目标向
量 G+Gc;然后,利用适应值赋值法对个体及目标向量进行评价,截断选择产生新子代种群和新子代目标向量,如
Step 1,Step 2 所示.在进化前期,使算法在目标空间中尽可能搜索,不对种群进行偏好区域的设置,避免陷入局部
最优;在进化中后期,利用偏好选择策略确定偏好区域并对偏好区域内个体进行适应值评价,如 Step 3,Step 4 所
示.在此过程中,决策者可通过修正参考点及β值修改偏好区域的位置及大小.其具体步骤如下所示.