Page 45 - 《振动工程学报》2025年第9期

第 9 期 毛晨洋，等：路面不平顺作用下具有不确定参数车辆系统随机振动分析 1975

0.15
MC
PDD-PEM
概率密度 10 −2 0 0.10
2
10
10
概率密度
10 2
10 0 0.05
20
15
10 −2 10
5
0 频率 / Hz 0 0 5 10 15 20 25
(a) 三维图像 加速度功率谱标准差 / [(m·s ) ·Hz ]
−1
−2 2
加速度功率谱 / [(m·s −2 ) 2 ·Hz −1 ]
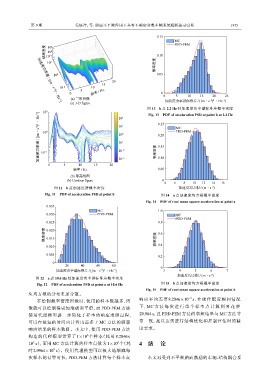
(a) 3-D figure
图 13 b 点 2.2 Hz 处加速度功率谱标准差概率密度
2
10
加速度功率谱 / [(m·s −2 ) 2 ·Hz −1 ] 10 0 10 1 0 1 −2 0.25 MC
Fig. 13 PDF of acceleration PSD at point b at 2.2 Hz
2
10

PDD-PEM
10
0.20
10
0.15
10
−2
10
0 5 10 15 20 10 −3 概率密度 0.10
频率 / Hz 0.05
(b) 等高线图
(b) Contour figure 0
4 6 8 10 12 14 16
−2
图 11 b 点加速度谱概率密度 加速度均方根 / (m·s )

Fig. 11 PDF of acceleration PSD at point b 图 14 a 点加速度均方根概率密度
Fig. 14 PDF of root mean square acceleration at point a

0.035

MC 1.0
0.030 PDD-PEM MC
PDD-PEM
0.025 0.8
概率密度 0.020 概率密度 0.6
0.015
0.010 0.4

0.005
0.2
0
20 40 60 80 0
−1
−2 2
加速度功率谱标准差 / [(m·s ) ·Hz ] 3 4 5 6 7

−2
加速度均方根 / (m·s )
图 12 a 点 10.6 Hz 处加速度功率谱标准差概率密度
Fig. 12 PDF of acceleration PSD at point a at 10.6 Hz 图 15 b 点加速度均方根概率密度
Fig. 15 PDF of root mean square acceleration at point b
应均方根的分布更加分散。
−4
在绘制概率密度图像时，使用的样本数越多，图 响应平均需要 8.2046×10 s，在硬件配置相同情况
像就可以绘制得更加准确和平滑，而 PDD-PEM 方法 下， MC 方 法 每 次 进 行 单 个 样 本 点 计 算 则 要 花 费
使用代理模型进一步简化了样本的响应求解过程， 29.964 s，且 PDD-PEM 方法的求解结果与 MC 方法非
可以在极短的时间内计算出远多于 MC 方法的频率 常一致，足以达到进行结构优化和控制评估时的精
响应结果的样本数目。本文中，使用 PDD-PEM 方法 度要求。

6
构造的代理模型计算了 1×10 个样本（耗时 8.2046×
4
10 s），而用 MC 方法计算的样本点数为 1×10 个（耗 4 结 论
2
5
时 2.9964×10 s）。使用代理模型可以极大地缩减每
次样本的计算时长，PDD-PEM 方法计算每个样本点 本文对受到不平顺路面激励的车辆-结构耦合系