Page 44 - 《振动工程学报》2025年第9期

1974 振 动 工 程 学 报 第 38 卷

率和计算精度，并且可以通过构造代理模型查看随 以发现频点在 2.2 Hz 附近时，加速度功率谱的概率
机函数的概率密度分布情况，应用范围更加广泛。 密度值较小，与图 7(b) 的加速度谱标准差曲线的峰
值相对应；而在 1.7 Hz 和 10.6 Hz 频点附近，加速度

COV=0.15 谱概率密度值最为分散。
2
10
加速度功率谱均值 / [(m·s −2 ) 2 ·Hz −1 ] 10 −1 0 MC(10 samples) 概率密度 10 10 −2 2 2 0

1
10
10
10
10
4
−2
10
0
10
PDD-PEM(V=2)
PDD-PEM(V=1)
−3
10
0 2 4 MPM 8 10 12 14 16 18 20 加速度功率谱 / [(m·s −2 ) 2 ·Hz −1 ] −2 15 20
6
10 10
频率 / Hz 5
0
频率 / Hz
图 8 变异系数为 0.15 时，不同方法计算的加速度功率谱均值
(a) 三维图像
Fig. 8 COV=0.15, mean of acceleration PSD by different methods (a) 3-D figure

COV=0.3 7 6 5 ×10 −3 10 2 10 2 1
2
10
加速度功率谱均值 / [(m·s −2 ) 2 ·Hz −1 ] 10 −2 0 6 4 MPM 17.5 18.0 18.5 加速度功率谱 / [(m·s −2 ) 2 ·Hz −1 ] 10 10 −2 0 10 0 1 −2
10
4
3
10
10
10
−3
4
2
MC(10 samples)
PDD-PEM(V=2)
10
PDD-PEM(V=1)
−4
10
6
0 1.9 2.0 2.1 2.2 8 10 12 14 16 18 20 0 5 频率 / Hz 15 20 10
2
4
(b) 等高线图
频率 / Hz
(b) Contour figure

图 9 变异系数为 0.3 时，不同方法计算的加速度功率谱均值
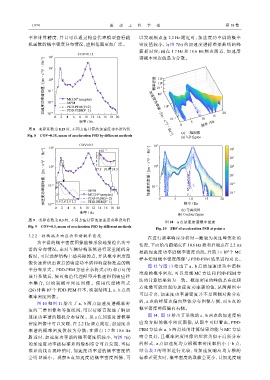
图 10 a 点加速度谱概率密度
Fig. 9 COV=0.3, mean of acceleration PSD by different methods
Fig. 10 PDF of acceleration PSD at point a

3.2.2 结构端点响应功率谱概率密度
在进行频率响应分析时一般较为关注峰值处的
功率谱的概率密度图像能够形象地描绘出功率
情况，下面给出前端点在 10.6 Hz 处和后端点在 2.2 Hz
谱的分布情况，在对车辆结构系统进行双重随机分
处的加速度功率谱概率密度曲线，并取 1×10 个 4 MC
析时，可以选择结构上感兴趣的点，并从概率密度图
样本绘制概率密度图像与 PDD-PEM 结果进行对比。
像快速辨识出该点的响应功率谱和响应标准差的概
图 12 与图 13 给出了 a、b 点的加速度功率谱标
率分布形式。PDD-PEM 方法在求得式 (15) 和 (16) 的
准差的概率密度，可以发现 MC 方法和 PDD-PEM 方
展开系数后，便可构造代理模型并快速得到响应样
法的计算结果较为一致。概率密度的峰值是在此频
本 集 合， 以 绘 制 概 率 密 度 图 像 。 使 用 代 理 模 型 式
点处最可能出现的加速度功率谱的值，从两幅图中
(26) 计算 10 个 6 PDD-PEM 样本，绘制结构上 a、b 点的
可以看出，加速度功率谱密度并不是两侧对称分布
概率密度图像。
的，a 点的峰值点偏向整体分布图像左侧，而 b 点的
图 10 和图 11 给出了 a、b 两点加速度谱概率密
度的三维图像和等值线图，可以清晰直观地了解加 概率密度峰值偏向右侧。
速度功率谱的随机分布情况。从 a 点加速度谱概率 图 14、图 15 给出了系统的 a、b 两点的加速度响
密度图像中可以发现，在 2.2 Hz 频点附近，加速度功 应均方根的概率密度图像，从图中可以看出，PDD-
率谱的概率密度值较为分散；在频点 1.7 和 10.6 Hz PEM 方法在 a、b 两点处的计算结果均能与 MC 方法
附近时，加速度功率谱的概率密度值较小，与图 7(a) 吻合良好，且概率密度图像的形状类似于高斯分布
的加速度功率谱标准差图像相结合可以发现，当标 的形式，a 点加速度均方根概率密度取值小于 b 点，
准差曲线出现峰值时，加速度功率谱的概率密度值 结合表 3 的结果进行比较，当加速度响应均方根的
会明显减小。观察 b 点加速度谱概率密度图像，可 标准差更大时，概率密度的取值会更小，且加速度响