Page 41 - 《振动工程学报》2025年第9期
P. 41
第 9 期 毛晨洋,等:路面不平顺作用下具有不确定参数车辆系统随机振动分析 1971
动功率谱响应的代理函数模型,如下式所示: 10 0
U ∑ N−k+1 q
∑ N ∑ ∑
˜ S U ( f,ε) =S 0 ( f)+ ··· ···
k=1 i 1 =1 i k =i k−1 +1 j 1 =1 10 −5
q
∑ k ∏ 位移功率谱 / (m 2 ·Hz −1 )
( )
A ( f)× ψ j l ε i l (26)
i 1 ···i k j 1 ··· j k −10
j k =1 l=1 10
上式中所有参数及表达式均已知,在每个频点
f 处,将结构随机参数样本代入 ˜ S U ( f,ε)中,便可准 10 −15
0 10 20 30 40
确、高效地获得随机响应功率谱的在每个频点的样 频率 / Hz
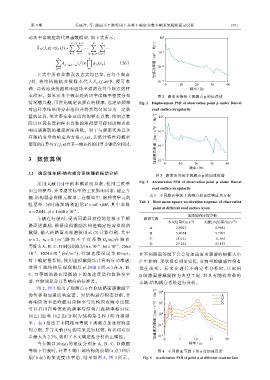
本结果。如果对某个频点处的功率谱概率密度分布 图 2 路面 B 等级下观测点 p 的位移谱
情况感兴趣,可首先确定该频点的频率,选定该频率 Fig. 2 Displacement PSD of observation point p under B-level
对应样本结果的分布范围并将其均匀划分为一定数 road surface irregularity
量的区段,统计落在各区段内的样本点数,使用点数 10 2
除以区段长度和样本总数的乘积便可得到该频点处
响应谱离散的概率密度函数。对于与频率无关且含 10 −0
有随机变量的响应均方根 σ (ε),其统计特性和概率
y 加速度功率谱 / [(m·s −2 ) 2 ·Hz −1 ]
密度的计算与 S ( f,ε)在某一频点处的计算步骤完全相同。 10 −2
3 数 值 算 例 10 −4
频率 / Hz
0 10 20 30 40
3.1 确定性车辆-结构耦合系统随机振动分析
图 3 路面 B 等级下观测点 p 的加速度谱
采用文献 [16] 中的车辆系统参数,使用二维垂 Fig. 3 Acceleration PSD of observation point p under B-level
road surface irregularity
向空间模型,并考虑实际中的主要影响因素,建立车
表 1 不同路面等级下观测点加速度响应均方根
辆-结构耦合有限元模型。在模型中,除弹簧单元的
Tab. 1 Root mean square acceleration response of observation
阻尼外,同时施加瑞利阻尼 C = αK +βM,其中参数
point at different road surface levels
−4
α = 2.044 β = 1.640×10 。
,
加速度响应均方根
车辆在行驶时,受到同源异相位的位移不平顺 路面等级
−2
−2
本文结果/(m·s ) 文献[16]结果/(m·s )
路面谱激励,根据虚拟激励法构造确定性虚拟简谐
A 2.9027 2.9681
激励,输入的路面功率谱使用式 (3) 计算得到,其中 B 5.8054 5.7991
w = 2,n 0 = 0.1 m ;路 面 不 平 度 系 数 G q (n 0 )在 路 面 C 11.611 11.561
−1
D 23.222 23.153
−6
−6
等级为 A、B、C、D 时分别取为 16×10 、 64×10 、 256×
−6
2
10 、 1024×10 −6 ( m /m −1 ) , 行 驶 速 度 设 定 为 10 m/s。 在不同路面等级下只会对加速度功率谱的幅值大小
对于确定性系统,使用虚拟激励法计算响应功率谱, 产生影响,形状没有明显变化,对频率的敏感性没有
求得车载结构后端观测点 p(如图 1 所示)在 A、B、 发 生 改 变 。 后 文 在 进 行 不 确 定 性 分 析 时, 只 取 用
C、D 等级的路面谱激励下的加速度谱和位移功率 B 级路面谱激励作为典型工况,对具有随机参数的
谱,在频域积分计算响应的标准差。 车辆-结构耦合系统进行分析。
图 2、图 3 给出了观测点 p 在 B 级路面谱激励下 4
的位移和加速度响应谱。对结构进行模态分析,并 10 A
B
将响应功率谱峰值对应频率与结构固有频率比较, 10 2 C
D
可以看出在峰值处的频率与结构自振频率相对应,
如 2.1 Hz 和 10.2 Hz 分 别 为 结 构 第 2 和 3 阶 自 振 频 加速度功率谱 / [(m·s −2 ) 2 ·Hz −1 ] 10 0
率。表 1 给出了不同路面等级下观测点加速度响应 10 −2
均方根,并与文献 [16] 的结果进行比较,两者相对误
差最大为 2.3%,表明了本文确定性分析的正确性。 10 −4 0 5 10 15 20
当车辆以 10 m/s的速度分别在 A、B、C、D 路面 频率 / Hz
等级下行驶时,计算车辆上部结构的前端(a 点)和后 图 4 不同路面等级下的 a 点加速度谱
端(b 点)的加速度功率谱,结果如图 4、图 5 所示。 Fig. 4 Acceleration PSD of point a at different road surface