Page 42 - 《振动工程学报》2025年第9期

1972 振 动 工 程 学 报 第 38 卷

加速度功率谱 / [(m·s −2 ) 2 ·Hz −1 ] 10 −2 0 D 构前、后端点加速度响应在系统不确定性参数影响
10 2 A 算结果的参考。

B
3.2.1 结构端点响应统计特征
C
考虑车辆模型参数具有的随机性，研究车载结
10
下的统计特征，结构的前、后端点为图
所示的
a、
1
方法分别计算
两点的加
两点。采用
PDD-PEM
a、b
b
−4
10
0
5
10
进行数值模拟验证结果的准确性和高效性。
频率 / Hz 15 20 速度功率谱密度均值和标准差，同时使用 MC 方法

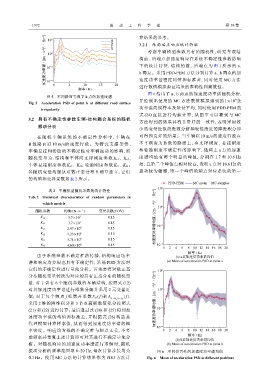
图 6 给出了 a、b 两点的加速度功率谱随机分析，
图 5 不同路面等级下 b 点的加速度谱
4
并绘制出使用的 MC 方法数值模拟得到的 1×10 条
Fig. 5 Acceleration PSD of point b at different road surface
功率谱曲线样本及统计平均，同时使用 PDD-PEM 的
irregularity
式 (24) 直接进行均值计算，从图中可以看到与 MC
3.2 具有不确定性参数车辆-结构耦合系统的随机
方法得到的结果具有非常好的一致性，表明采用较
振动分析
少的变量近似的维数分解和较低维度的降维积分即
在 随 机 车 辆 系 统 的 不 确 定 性 分 析 中， 车 辆 在 可得到良好的结果。当车辆以 10 m/s的速度行驶在
B 级 路 面 以 10 m/s的 速 度 行 驶 。 为 研 究 支 撑 条 件 、 不平顺度为 B 级的路面上，在支撑刚度、悬挂刚度
车辆悬挂和轮胎的不确定性对车辆振动的影响，取 和轮胎刚度不确定性的影响下，结构上 a 点的加速
随机变量为：结构和车体间支撑刚度参数 K c1 、K c2 ， 度谱均值有两个明显的峰值，分别在 1.7 和 10.6 Hz
、
车体悬挂刚度参数 K s1 、K s2 ，轮胎刚度参数 K t1 K t2 。 处，且第二个峰值点相对较高，表明 a 点对 10.6 Hz 的
各随机变量均服从对数正态分布且相互独立，它们 振动较为敏感，第一个峰值的频点对应系统的第一
的均值和变异系数如表 2 所示。
PDD-PEM MC mean MC-samples
10 2
表 2 车辆模型随机参数的统计特性
Tab. 2 Statistical characteristics of random parameters in
vehicle models
10 0
随机参数 均值/( N·m ) 变异系数(COV)
−1
3.7×10 7 0.15 加速度功率谱均值 / [(m· −2 ) 2 ·Hz −1 ]
K c1
K c2 3.7×10 7 0.15 10 −2
2.47×10 6 0.15
K s1
K s2 4.23×10 6 0.15
3.74×10 6 0.15
K t1
K t2 4.60×10 6 0.15 10 −4
0 2 4 6 8 10 12 14 16 18 20

频率 / Hz
由于系统参数不确定性的传播，结构响应功率 (a) a点加速度功率谱均值
谱和响应均方根也具有不确定性，采用 PDD 方法对 (a) Mean of acceleration PSD at point a
它们的不确定性进行量化分析。首先要将对数正态 10 2
分布随机变量转换为对应的具有正态分布的随机变
量，对于含有 6 个随机参数的车辆结构，按照式 (12)
对其加速度功率谱进行维数分解并采用 2 元变量近 10 0
似；对于每个频点 f 处展开系数 S 0 ( f)和 A ( f)，
i 1 ···i k j 1 ··· j k 加速度功率谱均值 / [(m· −2 ) 2 ·Hz −1 ]
采用 2 维的降维积分和 3 节点高斯数值积分按照式
(21) 和 (22) 进行计算；最后通过式 (24) 和 (25) 得到加 10 −2
速度功率谱的均值和标准差，并根据式 (26) 构造其
代理模型计算样本值，从而得到加速度功率谱的概 −4
率密度。响应均方根的不确定性与频点无关，不考 10 0 2 4 6 8 10 12 14 16 18 20
虑频率并重复上述计算即可对其进行不确定量化分 频率 / Hz
(b) b点加速度功率谱均值
析。对随机响应的加速度功率谱进行求解时，随机 (b) Mean of acceleration PSD at point b

振动分析的频率范围取 0~20 Hz，每次计算步长均为 图 6 不同位置处的加速度功率谱均值
0.1 Hz。使用 MC 方法的计算结果作为 PDD 方法计 Fig. 6 Mean of acceleration PSD at different positions