Page 43 - 《振动工程学报》2025年第9期

第 9 期 毛晨洋，等：路面不平顺作用下具有不确定参数车辆系统随机振动分析 1973

个固有频率，而第二个峰值对应的频点在第三个固 示，a 点的加速度均方根的均值大于 b 点，a 点加速度
有频率 10.26 Hz和第四个固有频率 10.85 Hz之间。结 均方根的标准差也大于 b 点，表明 a 点的加速度在双
构上 b 点的加速度谱均值仅在 2.2 Hz处有一个较为 重随机作用影响下随机误差区间更大。在表 3 中将
明显峰值，说明 b 点对 2.2 Hz的振动更为敏感，且此 PDD-PEM 方法与 MC 方法的计算结果进行比较，最
频点对应系统的第二阶固有频率。 大相对误差为 0.14%，表明了 PDD-PEM 方法在计算
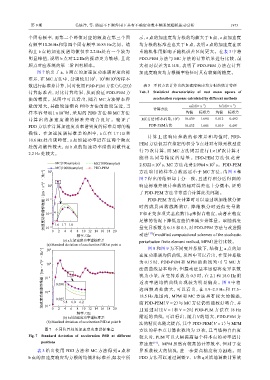
图 7 给出了 a、b 两点的加速度功率谱密度的标 加速度响应均方根概率特征时具有较高的精度。
准差，在 MC 方法中，分别使用 10 、 10 和 10 的样本
3
4
2
数进行标准差计算，同时使用 PDD-PEM 方法（式 (25)） 表 3 不同方法计算出的加速度响应均方根的统计特征
计算标准差，对比计算结果，从而验证 PDD-PEM 方 Tab. 3 Statistical characteristics of root mean square of
法的精度。从图中可以看出，随着 MC 方法样本容 acceleration response calculated by different methods

−2
量的增大，其曲线逐渐向 PDD 方法的曲线靠近，当 a点/(m·s ) b点/(m·s )
−2
计算方法
样本容量取 1×10 时，采用的 PDD 方法和 MC 方法 均值 标准差 均值 标准差
4
计 算 出 的 加 速 度 谱 的 标 准 差 吻 合 良 好 。 验 证了 MC方法（样本容量： 10 ） 10.439 1.694 5.012 0.492
4
PDD 方法在计算加速度功率谱密度的标准差时的精 PDD-PEM方法 10.432 1.685 5.019 0.491

确性。在加速度谱标准差的图中，a 点在 1.7 Hz 和
计 算 上 述 响 应 参 数 的 标 准 差 和 均 值 时， PDD-
10.6 Hz 处出现峰值，a 点加速功率谱在这两个频点
PEM 方法仅需在指定的积分节点处对有限元模型进
处的离散性较大，而 b 点的加速功率谱的离散性在
4
行 73 次计算，而 MC 方法则需进行 1×10 次计算才
2.2 Hz 处较大。
能 得 出 同 等 精 度 的 结 果 。PDD-PEM 方 法 仅 花 费

MC(100samples) MC(1000samples) 3 5
2.8322×10 s，MC 方法花费 2.9964×10 s。PDD-PEM
MC(10000samples) PDD-PEM 方法取用的样本点数远远小于 MC 方法，由图 6 和
加速度功率谱标准差 / [(m·s −2 ) 2 ·Hz −1 ] 10 10 −2 0 5 响应标准差统计参数的相对误差也十分微小，证明
2
10
得出的结果却十分一致，且进行积分后得到的
图
7
方法非常适合计算此类问题。
了
PDD-PEM
方法在计算时可以通过增加维数分解
PDD-PEM
时 的 成 员 函 数 截 断 数
U、 降 维 积 分 时 近 似 变 量 数
−4 4
q来提高精度，或者在精度
V和正交多项式基底数目
10
0.3，对
方法与改进摄
量变异系数为
和
−6
PDD-PEM
0.15
10
2
6
0 3 1.6 1.7 1.8 8 10 12 14 16 18 20 足够的情况下降低这些值来减少计算量。取随机变
4
频率 / Hz 动法 [17] （modified computational schemes of the stochastic
(a) a点加速度功率谱标准差 perturbation finite element method，MPM）进行比较。
(a) Standard deviation of acceleration PSD at point a 速度功率谱均值曲线，从图中可以看出，在变异系数
和图
图
a 点的加
为不同变异系数下，结构上
8
9
加速度功率谱标准差 / [(m·s −2 ) 2 ·Hz −1 ] 10 10 −2 0 0.030 为 法的曲线基本吻合，但摄动法基本思想将变异系数
2
10
的 曲 线 均 可 与
和
方
时 ， PDD-PEM
MPM
MC
0.15
时，在
视为小量，在变异系数为
和
18.0 Hz 附
2.1
0.3
中将
近功率谱均值曲线出现较为明显偏差。图
9
1.9~2.3 Hz 和
这 两 频 点 处 放 大， 可 以 看 出 ， 在
17.5~
−4
10
和
方法具有较大的偏差，
V = 2）与
而
PDD-PEM（
MC
−6
10
2
4
方 法 在
且 通 过 对 比
V = 1和
0 0.025 5.8 6 6.0 8 6.2 10 12 14 16 18 20 18.5 Hz 范围内，MPM V = 2时 MC 方法仍然能较好吻合，并
18 Hz
PDD-PEM
频率 / Hz
(b) b点加速度功率谱标准差 附近的曲线，可以看出，随着 V的增大，PDD-PEM 方
(b) Standard deviation of acceleration PSD at point b
法的精度也随之提高，其中 PDD-PEM（ V = 1）与 MPM
图 7 不同位置处的加速度功率谱标准差 方法的样本点计算次数均为 13 次，且当结构自由度
Fig. 7 Standard deviation of acceleration PSD at different 较大时，PEM 可以大幅提高每个样本点的功率谱计
positions [14]
算速度 。MPM 虽然有较高的计算效率，但对于变
表 3 给出使用 PDD 方法和 MC 方法得到 a 点和 异系数较大的情况，进一步提高精度较为困难。而
b 点的加速度响应均方根的均值和标准差,如表中所 PDD 方法可以通过调整 V、U和 q灵活地调整计算效