Page 23 - 《振动工程学报》2025年第9期

第 9 期 张理昊，等：基于边界条件等效的载荷传递结构动力学拓扑优化 1953

A B

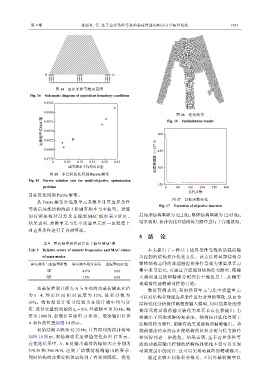
图 14 边界条件等效示意图
Fig. 14 Schematic diagram of equivalent boundary conditions

0.9925

0.9900
图 16 优化结果
主振型平均MAC值 0.9850 600
Fig. 16 Optimization results
0.9875

0.9825

0.9800 450
0.9775 动柔度模值 / (×10 −3 J)
0 0.05 0.10 0.15 0.20 0.25
固有频率平均相对误差
300
图 15 多目标优化问题 Pareto 解集
Fig. 15 Pareto solution sets for multi-objective optimization
150
problem 0 80 160 240 320 400
迭代步数
目标优化问题 Pareto 解集。
图 17 目标函数变化
从 Pareto 解集中选取单元参数并计算边界条件
Fig. 17 Variation of objective function
等效后局部结构的前 2 阶固有频率与主振型。计算
固 有 频 率 相 对 误 差 及 主 振型 MAC 值 如 表 9 所 示 。 后局部结构基频为 12.2 Hz，整体结构基频为 12.05 Hz。
结果表明，弹簧单元与集中质量单元在一定程度上 结果表明，拓扑优化对结构传力路径进行了合理规划。

对边界条件进行了合理等效。
5 结 论

表 9 固有频率相对误差及主振型 MAC 值
Tab. 9 Relative errors of natural frequencies and MAC values 本文提出了一种基于边界条件等效的动载荷输
of main modes 出控制的结构拓扑优化方法。该方法将局部结构与

固有频率与主振型阶数 固有频率相对误差 主振型MAC值 整体结构之间的非理想边界条件等效为弹簧单元与
1阶 4.6% 0.98 集中质量单元，再通过合理规划结构传力路径，使输
2阶 10% 0.98 入载荷通过结构精确分配到若干输出点上，从而实
现载荷传递精确可控的目的。
动载荷控制目标为 A 与 B 处的动载荷输出比值
数值算例表明，利用弹簧单元与集中质量单元
为 5∶4， 约 束 区 间 相 对 宽 度 为 15%， 体 积 分 数 为 可以对结构非理想边界条件进行合理的等效，从而为
60%。 将 初 始 设 计 变 量 设 置 为 在 设 计 域 中 均 匀 分 结构优化分析提供高精度输入模型，同时边界处的弹
布，设计变量的初始值 η e = 0.6，外载频率为 20 Hz，幅 簧单元将动载荷输出转化为单元节点位移输出，有
值为 1000 N，加载位置如图 13 所示。载荷输出位置 效减小了问题求解的复杂度。结构拓扑优化得到了
A 和 B 的位置如图 14 所示。 清晰的传力路径，能够有效实现载荷的精确输出。动
初始结构基频为 82.35 Hz，计算得到的拓扑构型 载荷输出约束的存在使结构的材料分配与传力路径
如图 16 所示，而结构动柔度模值变化如图 17 所示。 布局得到进一步优化。结果表明，基于边界条件等

在优化结果中，A、B 处输出载荷的幅值大小分别为 效的动载荷输出控制的结构拓扑优化不仅可以实现
379.35 和 356.98 N，达到了动载荷精确输出的要求， 动柔度最小的设计，还可以实现动载荷的精确输出。
同时结构的动柔度模值也得到了有效的降低。优化 通过比较不同体积分数比、不同外载荷频率以