Page 139 - 《振动工程学报》2025年第9期

第 9 期 汪殊楠，等：压电层合结构中 Love 波的传播及其在质量传感中的应用研究 2069

14
性，这为实际工程中 Love 波的求解提供了很大程度
12
的方便。
(2)
10 kH =1
(2)
3800 8 kH =2.5
(2)
kH =5
3600 Δc′ / (m·s −1 ) 6
3400 式(12) 4
3200
c / (m·s −1 ) 3000 式(17) 2 0
式(13)
2800
2600
(2)
H / H
2400 0 0.02 0.04 (3) 0.06 0.08 0.10
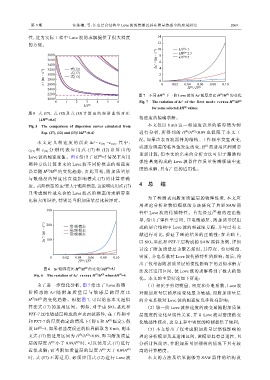
2200 图 7 不同 kH 下一阶 Love 波的 Δc′随厚度比 H /H 的变化
(2)
(3)
(2)
2000
(3)
0 1 2 3 4 5 6 Fig. 7 The variation of Δc′ of the first mode versus H /H (2)
kH (2)
(2)
for some selected kH values
图 5 式 (17)、 式 (12) 及 式 (13) 计 算 出 的 频 散 曲 线 对 比
相速度的精确求解。
（kH =0.4）
(3)
本文仅以 8 m/s 这一相速度误差的临界值为例
Fig. 5 The comparison of dispersion curves calculated from
(3)
(2)
Eqs. (17), (12) and (13)（kH =0.4） 进 行 分 析， 所 得 到 的 H /H <0.09 也 仅 限 于 本 文 工
(3)

况，如果声表面波器件的结构、工作频率发生改变，
本 文 定 义 相 速 度 的 误差 Δc′= c (17) −c (12) ， 其 中 ，
(3)
或速度误差的临界值发生改变，H 的适用区间需要
c (17 和 ) c (12 分 别 代 表 应 用 式 (17) 和 (12) 计 算 出 的
)
重新计算；但本文给出来的分析方法可用于薄膜和
(2)
Love 波的相速度值。图 6 给出了 kH =5 情况下应用
弹性基底构成的 Love 波器件在质量传感领域中速
两种方法计算出来的 Love 波不同阶模态的相速度
度的求解，具有广泛的适用性。
(2)
误差随 H /H 的变化趋势，由此可见，附加质量层
(3)
与敏感层的厚度比直接影响着式 (17) 的计算准确
4 总 结
度。高阶模态的 Δc′要大于低阶模态，这说明应用式 (17)
只考虑惯性效应会给 Love 波高阶模态的求解带来
为了检测表面附加质量层的物理性质，本文应
比较大的误差，特别是当附加质量层比较厚时。
用理论分析和数值模拟的方法研究了典型 SAW 器

300
件中 Love 波的传播特性。首先经过严格的理论推
导，给出了弹性半空间、压电敏感层、附加质量层组
Δc′ / (m·s −1 ) 100 第1阶模态 成的层合结构中 Love 波的相速度方程，并与已有文
200
第2阶模态
第3阶模态
献进行对比，验证了理论结果的正确性；在基础上，
以
层构成的
器件为例，详细
SiO 2 基底和
SAW
PZT-7
讨论了附加质量层为聚乙烯时，其厚度、剪切模量、
0 0.02 0.04 0.06 0.08 0.10 密度、介电系数对 Love 波传播特性的影响；最后，给
(3)
H / H (2)
出了仅考虑附加质量层的惯性影响下的近似求解方

图 6 Δc′随厚度比 H /H 的变化（kH =5）
(2)
(3)
(2)
法及其适用区间，使 Love 波的求解得到了极大的简
(3)
(2)
(2)
Fig. 6 The variation of Δc′ versus H /H when kH =5
化。本文的主要结论如下所述：
为了进一步量化分析，图 7 给出了 Love 波第一 （1） 相比于剪切模量、密度和介电系数，Love 波
阶 模 态的 Δc′ 随 附 加 质 量 层 与 敏 感 层 的 厚 度 比 对附加质量层的厚度变化最为敏感，而附加质量层
H /H 的变化趋势。根据图 7，可以给出本文近似 的介电系数对 Love 波的相速度几乎没有影响；
(3)
(2)
算法式 (17) 的适用区间。例如，对于由 SiO 2 基底和 （2） 第一阶 Love 波相速度的改变量随附加质量
PZT-7 压电敏感层构成的声表面波器件，在工作频率 层密度的变化呈线性关系，并且 Love 波对密度的变
和 PZT-7 的厚度确定的情况下（即 k 和 H 恒定)，假 化敏感性较高，这为工程中密度的检测提供了便利；
(2)
(2)
设 kH =5，如果相速度误差的临界值取为 8 m/s，则本 （3） 本文给出了仅考虑附加质量层惯性影响的
(3)
(2)
文式 (17) 的适用区间为 H /H <0.09，即当附加质量 理论分析模型及其适用区间，该模型具有普适性，且
层的厚度 H 小于 0.09H 时，可以使用式 (17) 进行 分析计算简洁，在附加质量层很薄的情况下具有较
(2)
(3)
近似求解；而当附加质量层的厚度 H 大于 0.09H (2) 高的计算精度。
(3)
时，式 (17) 不再适用，必须应用式 (12) 进行 Love 波 本文的方法及结果能够为 SAW 器件的结构设