Page 138 - 《振动工程学报》2025年第9期

2068 振 动 工 程 学 报 第 38 卷

由此可见：剪切模量的增加、密度和介电系数的减
小均会使 Love 波传播得更快，这是因为三者会同时 3 低 频 情 况 下 的 近 似 求 解
增加整体结构的等效剪切模量；此外，Love 波对附加
质量层的剪切模量和密度的变化敏感性更高，对介 由上述分析可见，由 SiO 2 和 PZT-7 构成的声表
电系数的敏感性有所降低，即图 4(a) 和 (b) 中相速度 面器件可以用来检测附加质量层的厚度及材料参
的改变量要大于图 4(c)，这是因为附加质量层直接与 数；但其相速度方程 (12) 过于复杂，这给问题的求解
压电敏感层相接触，其附加的电场对器件本身电场 带来了诸多不便。为了简化模型，同时考虑到工程
影响很小。值得注意的是，图 4(b) 中 Δc 与密度的变 应用中附加质量层的厚度很小，本文仅考虑附加质
化趋势呈线性，并且 Love 波对密度的变化敏感性较 量层的惯性影响，即 [25] ：
高，因此，只需通过不同直线的斜率即可较为精确地
(2)
(2)
(2)
(3)
¨
x = −H (2) : σ = ρ 3 H w ,D = 0 （15）
zx
x
推断出密度的改变量，无需重复测量，这给工程应用
于是，将理论解 (3)~(6) 代入到 x=0 的连续性条件及
中密度的检测带来了诸多便利。综合图 4，SiO 2 和
式 (15)，可得：
PZT-7 组成的声表面波器件更合适于检测附加质量 
A 1 = A 3

的厚度、弹性系数及密度。 



 A 2 = e 15 A 3 /ε 11 + A 5





kH =1 kH =2  ¯c 44 b 2 A 4 +e 15 A 6 +µ 1 b 1 A 1 = 0

(2)
(2)





(2)
(2)
(2)

kH =3 kH =4 kH =5 ε 1 A 2 +ε 11 A 6 = 0

10  (2) (2)
 ¯c 44 [A 4 cosh(kb 2 H )b 2 − A 3 sinh(kb 2 H )b 2 ]+





 (2) (2)
 e 15 [A 6 cosh(kH )− A 5 sinh(kH )] =


5

Δc / (m·s −1 ) 0  ε 11 [A 6 cosh(kH )− A 5 sinh(kH )] = 0 (2)


(2)
2
(3)
ρ 3 H kc [A 4 sinh(kb 2 H )− A 3 cosh(kb 2 H )]






(2)
(2)

（16）
−5
该方程组有非零解的条件是方程组系数矩阵行列式
−10
为零，由此可得相速度方程为：
0 1 2 3 4 5 [
μ 3 / GPa [ (3) 2 ( (2) )]
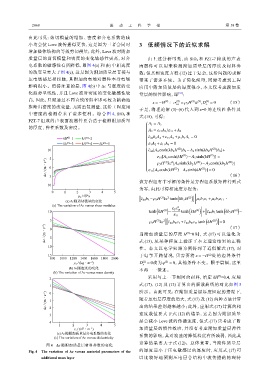
(a) Δc随剪切模量的变化 ¯ c 44 b 2 −ρ 3 H kc tanh kb 2 H µ 1 b 1 ε 1 +µ 1 b 1 ε 11 ·
(a) The variation of Δc versus shear modulus ]
( ) ε 1 e 2 ( ) [ ( )
10 tanh kH (2) − 15 tanh kH (2) + ¯c 44 b 2 tanh kb 2 H (2) −
ε 11
][ ( )]
5 (3) 2 (2)
ρ 3 H kc ¯ c 44 b 2 ε 1 + ¯c 44 b 2 ε 11 tanh kH =0 （17）
Δc / (m·s −1 ) −5 0 当附加质量层的厚度 H =0 时，式 (17) 可以退化为
(3)
−10 式 (13)，从某种程度上验证了本文理论结果的正确
性。本文以电学短路为例得到了近似解式 (17)，对
−15 于电学开路情况，只需要将 x = −H 处的边界条件
(2)
800 1000 1200 1400 1600 1800 2000
(2)
(2)
−3
ρ 3 / (kg·m ) D = 0改为 φ = 0，其他条件不变。限于篇幅，这里
x
(b) Δc随密度的变化 不再一一赘述。
(b) The variation of Δc versus mass density
采用与上一节相同的材料，给定 kH =0.4，应用
(3)
2
(17)、(12) 及
(13) 计算出的频散曲线的对比如图
5
1 0 式 所示。由此可见：在附加质量层厚度恒定的情况下，
Δc / (m·s −1 ) −1 随着压电层厚度的增大，式 (17) 及 (12) 两种方法计算
(17) 计算的相
出的结果差别越来越小；此外，应用式
−2
−3 速度数值要大于式 (12) 的结果，这是因为附加质量
−4 层会减小 Love 波的传播速度，但式 (17) 只考虑了附
1 2 3 4 5
−1
ε 3 / (nF·m ) 加质量层的惯性效应，并没有考虑附加质量层弹性
(c) Δc随附加质量层介电系数的变化
(c) The variation of Δc versus dielectricity 系数的影响，其对波速的降低程度有所减弱，因此其

计算结果要大于式 (12)。总体来看，当附件质量层
图 4 Δc 随附加质量层材料参数的变化
的厚度远小于压电敏感层的厚度时，应用式 (17) 可
Fig. 4 The variation of Δc versus material parameters of the
additional mass layer 以比较好地预测压电层合结构中波传播的物理特