Page 126 - 《摩擦学学报》2021年第2期

第 2 期 尹兆明, 等: 基于热弹流润滑的双渐开线齿轮温度场研究 271

i
R 1j (t)

β b1
′
j N 1 N l
B l j β b1
Δl
l c
l b i
l a R 1j (t)
β b2
′
β b1
N 2 N 2
I H GN 2 B 2 F E C P D B 1 N 1

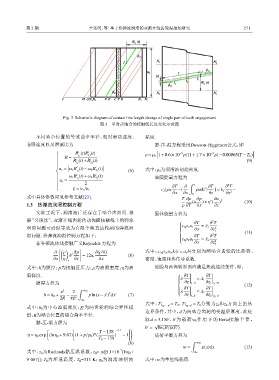
Fig. 3 Schematic diagram of contact line length change of single pair of teeth engagement
图 3 单对齿啮合的接触线长度变化示意图

不同啮合位置的等效曲率半径、相对滑动速度、 黏度.
卷吸速度以及滑滚比为 密-压-温方程采用Dowson-Higginson公式，即
 i i [ ]
 R (t)R (t) −9 −9
 2j ρ = ρ 0 1+0.6×10 p/(1+1.7×10 p)−0.00065(T −T 0 )
 1j
 R =

 i i
 R (t)+R (t) (9)

 1j 2j



 i i

 u s = ω 1 R (t)−ω 2 R (t) 式中： ρ 0为润滑油初始密度.
1j 2j (5)


 i i
 ω 1 R (t)+ω 2 R (t)
 油膜能量方程为
 2 j
 1j
 u r =


 2
 ∫ z
 2
 ∂T ∂ ∂T ∂ T
 ′
c f [ρu −( ρudz ) ] = k f −
ξ = u s /u r
∂x ∂x 0 ∂z ∂z 2
式中具体参数可见参考文献[23].
T ∂ρ ∂p ∂u
∗
(u )+η ( ) 2 (10)
1.3 热弹流润滑控制方程 ρ ∂T ∂x ∂z
实际工况下，润滑油广泛存在于啮合齿面间. 根 固体能量方程为
据“分段法”，双渐开线齿轮传动齿面接触线上的弹流  2
 ∂T ∂ T

润滑问题可近似等效为有限个薄直齿轮副的弹流润 c 1 ρ 1 u 1 = λ 1 2



 ∂x ∂z 1 (11)
2
滑问题. 热弹流润滑控制方程如下：  ∂T ∂ T




 ρ 2 u 2 = λ 2 2
c 2
非牛顿流体线接触广义Reynolds 方程为 ∂x ∂z 2
ρ
∂ [( ) 3 ∂p ] ∂(ρ h) 式中： c i ,ρ i ,u i ,k i (i = a,b)分别为两啮合齿轮的比热容、
∗
h = 12u r (6)
∂x η ∂x ∂x 密度、速度和热传导系数.
e
式中： h为膜厚； p为接触区压力； ρ为油膜密度； η为油 油膜与两齿轮界面应满足热流连续条件，即：
膜黏度.  ∂T
λ = λ 1
 ∂T


膜厚方程为  ∂z 1 z 1 =0

 ∂z z=0

 (12)
 ∂T
∫

 ∂T
x 2 2 x out ′ 2 λ = λ 2


h = h 0 + − pln(x− x ) dx ′ (7) ∂z z=h ∂z 2 z 2 =0

2R πE ′ x in
式中： T| z a =−d = T 0 T| z b =d = T 0 分别为 和 方向上的热
、
式中： h 0为中心油膜厚度； 为两齿轮的综合弹性模 z a z b
′
E
边界条件，其中， d为两啮合齿轮的变温层厚度，此处
量； R为啮合位置的综合曲率半径.
取 d = 3.15b b 为载荷 w 0 作用下的Hertz接触半宽，
，
′
′
黏-压-温方程为 √
b = 8w 0 R/(πE ).
′
′
{ [ −1.1 ]}
T −138
η = η 0 exp (lnη 0 +9.67) (1+ p/p 0 ) ( ) −1 载荷平衡方程为
z 0
T 0 −138
(8) ∫ x out
w = p(x)dx (13)
−9
式中：z 为Roelands黏压温系数，z = α/[5.1×10 (lnη + x in
0
0
0
9 067)]；T 为环境温度，T =313 K；η 为润滑油初始 式中： w为单位线载荷.
0
0
0