Page 67 - 《爆炸与冲击》2025年第9期

σ 3 −2.539 σ −5
σ σ −3.224
−10
−15
0.13
第 45 卷 周 鑫，等： 混凝土中柱形装药的爆炸破坏分区及应力波衰减规律 −1/3 第 9 期

−1/3

0.11
0.6 Stress 0.10 Stress
Fitting curve Fitting curve
0.5 0.09
0.08
0.4
0.07
0.3
σ m /GPa 0.2 σ m =0.024Z −1.84 R =0.996 1 σ m /GPa 0.06 σ m =0.034Z −1.452 R =0.999 3
2
2
0.05
0.04
0.1 0.03
0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.5 0.6 0.7 0.8 0.9 1.0
Z/(m·kg −1/3 Z/(m·kg −1/3
(c) Transition zone (d) Crack zone
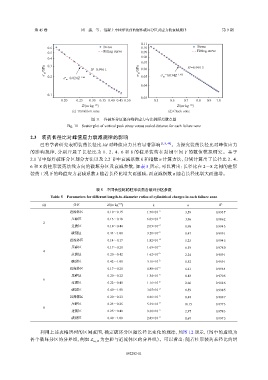
图 11 各破坏分区竖向峰值应力与比例距离散点图
Fig. 11 Scatter plot of vertical peak stress versus scaled distance for each failure zone

2.3 装药长径比对峰值应力衰减规律的影响
已有学者研究表明装药长径比 l/d 对峰值应力具有显著影响 [5, 8, 48] 。为探究装药长径比对峰值应力
的影响规律，分别开展了长径比为 1、2、4、6 和 8 的柱形装药在封闭空间下的数值模拟研究。基于

2.1 节中爆炸破坏分区划分方法以及 2.2 节中衰减系数 k 和指数 n 计算方法，分别计算出了长径比 2、4、
6 和 8 的柱形装药法线方向的破坏分区及衰减参数，如表 5 所示，可以看出：长径比在 2～8 之间的柱形
装药工况下的峰值应力衰减系数 k 随着长径比增大而递减，而衰减指数 n 随着长径比增大而递增。

表 5 不同长径比的柱形装药各破坏分区参数
Table 5 Parameters for different length-to-diameter ratios of cylindrical charges in each failure zone
l/d 分区 Z/(m·kg −1/3 ) k n R 2
近流体区 0.10～0.15 1.70×10 −3 3.59 0.993 7
压碎区 0.15～0.18 6.05×10 −4 3.96 0.986 2
2
过渡区 0.18～0.44 2.03×10 −2 1.98 0.994 3
破裂区 0.44～1.00 3.28×10 −2 1.47 0.999 1
近流体区 0.14～0.17 1.82×10 −4 5.25 0.994 5
压碎区 0.17～0.20 1.69×10 −5 6.59 0.978 0
4
过渡区 0.20～0.42 1.62×10 −2 2.24 0.989 1
破裂区 0.42～1.00 3.16×10 −2 1.52 0.999 1
近流体区 0.17～0.20 4.88×10 −5 6.61 0.996 4
压碎区 0.20～0.22 1.34×10 −6 8.83 0.970 5
6
过渡区 0.22～0.40 1.16×10 −2 2.66 0.982 6
破裂区 0.40～1.00 3.05×10 −2 1.59 0.998 5
近流体区 0.20～0.23 6.66×10 −6 8.49 0.989 7
压碎区 0.23～0.25 5.39×10 −7 10.15 0.977 3
8
过渡区 0.25～0.40 9.30×10 −3 2.97 0.978 3
破裂区 0.40～1.00 2.85×10 −2 1.67 0.997 5

利用上述表格所列的区间范围，确定破坏分区随长径比变化的规律，如图 12 所示，（图中的虚线为
各个破坏分区的分界线，例如 Z l 为空腔与近流体区的分界线）。可以看出：随着柱形装药长径比的增
ca, f

092202-11