Page 64 - 《爆炸与冲击》2025年第9期

第 45 卷 周 鑫，等： 混凝土中柱形装药的爆炸破坏分区及应力波衰减规律 第 9 期

50 5

0.32 m/kg 1/3 0.46 m/kg 1/3 0.55 m/kg 1/3
40 0.38 m/kg 1/3 0.50 m/kg 1/3
0
30
σ /MPa x 20 σ /MPa x −5 1/3
10
0.65 m/kg
0.75 m/kg 1/3
0 −10 0.85 m/kg 1/3
0.95 m/kg 1/3
−10 1.07 m/kg 1/3
−15
0 50 100 150 200 250 300 0 50 100 150 200 250 300 350 400
Time/μs Time/μs
(a) 0.32 m/kg ≤ Z ≤ 0.50 m/kg 1/3 (b) 0.65 m/kg ≤ Z ≤ 1.07 m/kg 1/3
1/3
1/3
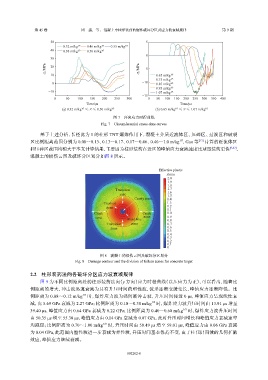
图 7 环向应力时程曲线
Fig. 7 Circumferential stress-time curves

基于上述分析，长径比为 1 的柱形 TNT 爆炸作用下，混凝土介质近流体区、压碎区、过渡区和破裂
1/3
区比例距离范围分别为 0.08～0.13、0.13～0.17、0.17～0.46、0.46～1.0 m/kg ，Gao 等 [12] 计算的近流体区
和压碎区范围均稍大于本文计算结果，主要因为柱形装药在近区的峰值应力衰减速度比球型装药更快 [9, 42] ，
混凝土的损伤云图及破坏分区划分如图 8 所示。

Effective plastic

strain
2.0
1.9
1.8
Transition 1.7
zone 1.6
1.5
Cavity zone 1.4
Crushed 1.3
zone 1.2
1.1
Crack Crack 1.0
zone Fluid-like zone 0.9
0.8
Transition zone 0.7
zone 0.6
0.5
0.4
0.3
0.2
0.1
0
图 8 混凝土的损伤云图及破坏分区划分
Fig. 8 Damage contour and the division of failure zones for concrete target

2.2 柱形装药法向各破坏分区应力波衰减规律
图 9 为不同比例距离处的柱形装药法向（y 方向）应力时程曲线（以压应力为正），可以看出，随着比
例距离的增大，冲击波迅速衰减为具有升压时间的塑性波，波形逐渐变缓变长，峰值应力逐渐降低。比
例距离为 0.08～0.12 m/kg 1/3 时，爆炸应力波为强间断冲击波，升压时间接近 0 μs，峰值应力呈现线性衰
减，由 5.69 GPa 衰减为 2.27 GPa；比例距离为 0.18～0.30 m/kg 1/3 时，爆炸应力波升压时间由 13.91 μs 增至
39.40 μs，峰值应力由 0.64 GPa 衰减为 0.22 GPa；比例距离为 0.40～0.60 m/kg 1/3 时，爆炸应力波升压时间
由 50.35 μs 增至 55.38 μs，峰值应力由 0.14 GPa 衰减为 0.07 GPa，此时升压时间增长和峰值应力衰减速率
均减缓；比例距离为 0.70～1.00 m/kg 1/3 时，升压时间由 58.49 μs 增至 59.01 μs，峰值应力由 0.06 GPa 衰减
为 0.04 GPa，此范围内塑性波进一步衰减为弹性波，升压时间基本保持不变，由于柱（球）面波的几何扩散
效应，峰值应力继续衰减。

092202-8