Page 68 - 《爆炸与冲击》2025年第9期
P. 68
第 45 卷 周 鑫,等: 混凝土中柱形装药的爆炸破坏分区及应力波衰减规律 第 9 期
大,近流体区、压碎区和过渡区逐渐变窄。图 13 为不同长径比柱形装药底部峰值应力(p )和空腔区边界
1
处峰值应力(p )的变化趋势图,可以发现:一方面,柱形装药长径比增大使得装药底部的峰值应力提升,
2
与文献 [28] 观点一致;另一方面,柱形装药长径比增大导致峰值应力衰减系数变大,应力衰减加快 [14] ,导
致空腔区边界处峰值应力(p )随装药长径比的增大而减小,进一步导致其他破坏分区变窄。
2
12
l/d p 1
0 1 2 3 4 5 6 7 8 9 11 p 2
0.05 10
0.10 Cavity zone Z ca,fl
Z fl,cr 9
0.15 Fluid-like zone Z cr,tr 8 TNT Blasting cavity
Crushed zone Z tr,cr p 1
0.20 σ m /GPa 7
Z/(m·kg −1/3 ) 0.25 6 5 Concrete
p 2
0.30
0.35 Transition zone 4
0.40 3 1 2 3 4 5 6 7 8
0.45 Crack zone l/d
图 12 破坏分区范围随着长径比的变化关系 图 13 装药底部及空腔壁处峰值应力变化趋势
Fig. 12 Failure zone boundaries versus ratio of Fig. 13 Peak stress in guage 1 and 2 versus
length to diameter ratio of length to diameter
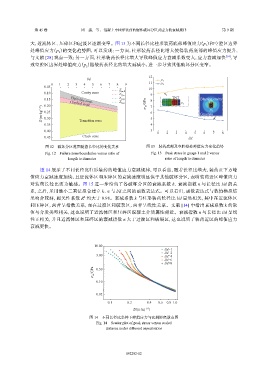
图 14 展示了不同长径比柱形装药的峰值应力衰减规律,可以看出,随着长径比增大,装药正下方峰
值应力衰减速度加快,且近流体区和压碎区的衰减速度明显快于其他破坏分区,表明装药近区峰值应力
对装药长径比更为敏感。图 15 进一步给出了各破坏分区的衰减系数 k、衰减指数 n 与长径比 l/d 的关
系,之后,采用最小二乘法拟合建立 k、n 与 l/d 之间的函数表达式。可以看出,函数表达式与数值模拟结
2
果吻合较好,相关性系数 R 均大于 0.98。衰减系数 k 与柱形装药长径比 l/d 呈负相关,其中在近流体区
和压碎区,两者呈指数关系,而在过渡区和破裂区,两者呈线性关系。文献 [14] 中指出衰减系数 k 的取
值与介质类型相关,这也说明了近流体区和压碎区混凝土介质属性相近。衰减指数 n 与长径比 l/d 呈线
性正相关,并且近流体区和压碎区的衰减指数 n 大于过渡区和破裂区,这也说明了装药近区的峰值应力
衰减更快。
10.00
l/d=1
3.00 l/d=2
l/d=4
l/d=6
l/d=8
σ m /GPa 0.50
0.10
0.02
0.1 0.2 0.4 0.6 0.8 1.0
Z/(m·kg −1/3
图 14 不同长径比条件下峰值应力与比例距离散点图
Fig. 14 Scatter plot of peak stress versus scaled
distance under different aspect ratios
092202-12