Page 70 - 《爆炸与冲击》2025年第9期

第 45 卷 周 鑫，等： 混凝土中柱形装药的爆炸破坏分区及应力波衰减规律 第 9 期

8 7

Simulation 6 Simulation
Eqs. (4)−(6) Eqs. (4)−(6)
6
4
σ m /GPa 4 σ m /GPa

2
2

0 0
0 0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0
Z/(m·kg −1/3 ) Z/(m·kg −1/3 )
(a) l/d=1 (b) l/d=2

6 6
Simulation Simulation
Eqs. (4)−(6) Eqs. (4)−(6)
4 4
σ m /GPa 2 σ m /GPa 2

0 0
0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0
Z/(m·kg −1/3 ) Z/(m·kg −1/3 )
(c) l/d=4 (d) l/d=6
6
Simulation
Eqs. (4)−(6)
4
σ m /GPa 2

0
0.2 0.4 0.6 0.8 1.0
Z/(m·kg −1/3 )
(e) l/d=8
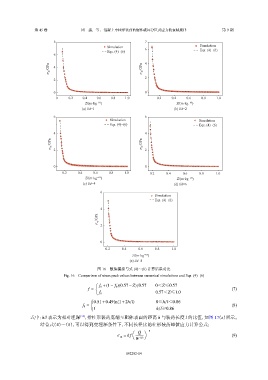
图 16 数值模拟与式 (4)～(6) 计算结果对比
Fig. 16 Comparison of stress peak values between numerical simulations and Eqs. (4)−(6)
®
f 0 +(1− f 0 )(0.57−Z)/0.57 0＜Z≤0.57
f = (7)
0.57＜Z≤1.0
f 0
®
0.51+0.49ln(1+2h/l) 0≤h/l＜0.86
f 0 = (8)
1 h/l≥0.86
式中：h/l 表示为相对埋深 [12] ，指柱形装药底端至靶体表面的距离 h 与装药长度 l 的比值，如图 17（a）所示。
结合式（4）～（8），可以得到变埋深条件下，不同长径比的柱形装药峰值应力计算公式：
Å ã −n
Q
σ m = k f (9)
W 1/3

092202-14