Page 66 - 《爆炸与冲击》2025年第9期

第 45 卷 周 鑫，等： 混凝土中柱形装药的爆炸破坏分区及应力波衰减规律 第 9 期

在防护工程抗爆设计中，峰值应力的最大 Simulation
n=1.739, spherical [44, 45] n=1.39, cylindrical [14]
值通常是设计者关注的重点，主要出现在常规武
n=1.734, spherical [13] n=2.38/1.734, cylindrical [12]
器法向 [12] （y 方向），因此后续研究中的峰值应力 15.00
σ 默认指代法向峰值应力。双对数坐标系下柱 5.00
m
形装药正下方的峰值应力 σ 与比例距离 Z 关系 A (0.13, 1.86)
m
如图 10 所示，可以看出，近流体区与压碎区的峰 σ /GPa 1.00 B (0.17, 0.72)
值应力衰减明显快于过渡区和破裂区，这表明单 m 0.30 C (0.46, 0.11)
Z=0.24
一衰减指数难以准确描述各个破坏分区的峰值 0.10 m/kg 1/3
应力衰减规律。王明洋等 [43] 和吴祥云等 [15] 基于 Fluid-like Crushed zone Transition Crack
0.02 zone zone zone
试验和数值模拟研究了岩石类介质中爆炸地冲
0.10 0.15 0.30 0.50 1.00
击传播规律，也发现装药近区（0～0.2 m/kg ）和
1/3
Z/(m·kg −1/3 )
中远区（0.2～1.0 m/kg ）的峰值应力衰减规律存
1/3
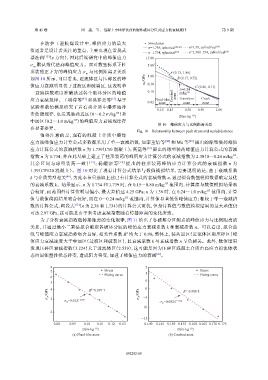
图 10 峰值应力与比例距离关系
在显著差异。
Fig. 10 Relationship between peak stress and scaled distance
值得注意的是，现有的混凝土介质中爆炸
应力波峰值应力计算公式多数都采用了单一衰减指数，如李重情等 [44] 和 Mu 等 [45] 提出的球型装药峰值
应力计算公式的衰减指数 n 为 1.739（C50 混凝土）；高矗等 [13] 提出的球型装药峰值应力计算公式的衰减
指数 n 为 1.734，并在此基础上建立了柱形装药的峰值应力计算公式的衰减指数为 2.38（0～0.24 m/kg ，
1/3
其 余 区 间 与 球 型 装 药 一 致 ） [ 12 ] ； 杨 耀 宗 等 [ 14 ] 提 出 的 柱 形 装 药 峰 值 应 力 计 算 公 式 的 衰 减 指 数 n 为
1.39（CF120 混凝土）。图 10 对比了现有计算公式结果与数值模拟结果，需要说明的是，由于衰减系数
k 与介质类型相关 [46] ，为此本节只选取上述已有计算公式的衰减指数 n，通过拟合数值模拟数据确定最优
的衰减系数 k。结果显示，n 为 1.734 和 1.739 时，在 0.15～0.80 m/kg 1/3 范围内，计算值与数值模拟结果吻
合较好，而范围外计算值明显偏小，最大差值达 4.25 GPa；n 为 1.39 时，在 0.24～1.0 m/kg 1/3 范围内，计算
值与数值模拟结果吻合较好，而在 0～0.24 m/kg 1/3 范围内，计算值显著低估峰值应力；相较于单一衰减指
数的计算公式，两段式 [12] （n 为 2.38 和 1.734）的计算公式更优，但是计算值与数值模拟结果的最大差值仍
可达 2.97 GPa，这可能是由于未考虑衰减指数随着传播距离的变化所致。
为了分析衰减指数随传播距离的变化规律，图 11 给出了各破坏分区测点的峰值应力与比例距离的
关系，并通过最小二乘法拟合确定各破坏分区的峰值应力衰减系数 k 和衰减指数 n。可以看出，拟合曲
线与峰值应力衰减趋势吻合良好，相关性系数 R 均大于 0.98；整体上，装药近区（近流体区和压碎区）峰
2
值应力衰减速度大于中远区（过渡区和破裂区），且衰减系数 k 与衰减指数 n 呈负相关。此外，数值结果
发现压碎区衰减指数（3.224）大于近流体区（2.539），这可能是因为压碎区混凝土介质由高应力拟流体状
态向固体塑性状态转变，造成阻力突变，加速了峰值应力的衰减 [47] 。

8 5
7 Stress Stress
Fitting curve 5 Fitting curve
6
0
5
2
σ m /GPa 4 R =0.997 7 σ m /GPa −5 0 R =0.980 8
2
3
σ m =0.01Z −2.539 −3.224
σ m =0.002Z
−10
2
−15
0.08 0.09 0.10 0.11 0.12 0.13 0.140 0.145 0.150 0.155 0.160 0.165 0.170 0.175
Z/(m·kg −1/3 Z/(m·kg −1/3
(a) Fluid-like zone (b) Crushed zone

092202-10
0.3 =0.999 3

σ σ σ =0.034 −
σ −

0.03
0.30 0.35
−1/3 −1/3