Page 62 - 《爆炸与冲击》2025年第9期

1.4
1.2
1.0
0.8
0.6
0.4
0.2
−2 −0.2
Time/μs
Time/μs
第 45 卷 周 鑫，等： 混凝土中柱形装药的爆炸破坏分区及应力波衰减规律 第 9 期
0.6

Gauge 1-2
0.5 Gauge 1-5
Gauge 2-2
0.4 Gauge 2-5
Gauge 3-2
Pressure/GPa 0.3 Simulation
Gauge 3-5
0.2
0.1
0
−0.1
0 20 40 60 80 100
Time/μs
(c) Third-layer measurement points
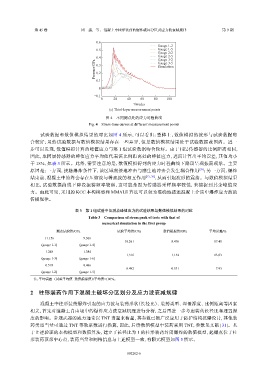
图 4 不同测点处的应力时程曲线
Fig. 4 Stress-time curves at different measurement points

试验数据和数值模拟结果的对比如图 4 所示，可以看出：整体上，数值模拟的波形与试验数据吻
合较好；虽然试验数据与数值模拟结果存在一些差异，但是数值模拟结果处于试验数据范围内。进一
步可以发现，数值模拟计算的峰值应力与第 1 组试验数据吻合较好。由于同层传感器的比例距离相同，
因此，取同层传感器的峰值应力平均值代表该比例距离处的峰值应力，进而计算出平均误差，其值均小
于 18%，如表 3 所示。此外，需要注意的是，数值模拟得到的应力时程曲线下降段呈现振荡现象。主要
原因是：一方面，接触爆炸条件下，该区域直接地冲击与感生地冲击会发生耦合作用 [29] ；另一方面，爆炸
结束前，混凝土中始终会存在压缩波与稀疏波的相互作用 [13, 30] ，从而引起波形的震荡。与数值模拟结果
相比，试验数据曲线下降段振荡频率较弱，这可能是因为传感器采样频率较低，未捕捉到其余峰值应
力。由此可见，采用的 KCC 本构模型和 MMALE 算法可以较为准确地描述混凝土介质中爆炸应力波的
传播规律。

表 3 第 1 组试验中各测点峰值应力的试验结果与数值模拟结果的对比
Table 3 Comparison of stress peak of tests with that of
numerical simulation in the first group
测点试验值/GPa 试验平均值/GPa 数值模拟值/GPa 平均误差/%
11.156 9.366
10.261 8.476 17.40
(gauge 1-1) (gauge 1-4)
1.248 1.384
1.316 1.134 13.83
(gauge 1-3) (gauge 1-6)
0.518 0.466
0.492 0.531 7.93
(gauge 1-2) (gauge 1-5)
注：平均误差=（试验平均值−数值模拟值）/平均值×100%。

2 柱形装药作用下混凝土破坏分区划分及应力波衰减规律

混凝土中柱形装药爆炸引起的应力波与装药形状（长径比）、装药类型、埋置深度、比例距离等因素
相关，首先对混凝土自由场中的爆炸应力波衰减机理进行分析，之后再进一步考虑装药长径比和埋置深
度的影响。常规武器的威力通常以 TNT 当量来衡量，其参数已被广泛应用于防护结构抗爆设计，其他装
药类型当量可通过 TNT 等效系数进行换算，因此，后续数值模型中装药采用 TNT，参数见文献 [31]。基
于上述验证的本构模型和数值算法，建立了长径比为 1 的柱形装药封闭爆炸的数值模型，起爆点位于柱
形装药顶部中心点，装药当量和网格信息与上述模型一致，有限元模型如图 5 所示。

092202-6