Page 71 - 《爆炸与冲击》2025年第9期
P. 71
第 45 卷 周 鑫,等: 混凝土中柱形装药的爆炸破坏分区及应力波衰减规律 第 9 期
Initiation point
f
l Cylindrical
h charge
1.0
Stage Ⅰ
Stage Ⅱ
f 0
Concrete
0 0.57 1.00 Z
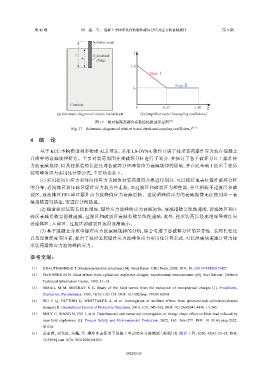
(a) Schematic diagram of relative burial depth (b) Simplified model forcoupling coefficient f
图 17 相对埋深及耦合系数简化模型示意图 [12]
Fig. 17 Schematic diagram of relative burial depth and coupling coefficient f [12]
4 结 论
基于 KCC 本构模型和多物质 ALE 算法,采用 LS-DYNA 软件开展了柱形装药爆炸应力波在混凝土
介质中的衰减规律研究。主要对装药周围介质破坏分区进行了划分,并探讨了各个破坏分区上爆炸应
力波衰减规律,以及柱形装药长径比对各破坏分区峰值应力衰减规律的影响,并在此基础上提出了柱形
装药峰值应力实用化计算公式,主要结论如下。
(1) 采用径向压应力和环向拉应力为阈值对装药周围介质进行划分,可以较好地表征爆炸破坏分区
的分布;近流体区和压碎区爆炸应力波为冲击波,而过渡区和破裂区为塑性波,并且相较于过渡区和破
裂区,近流体区和压碎区爆炸应力波峰值应力衰减更快。这说明峰值应力的衰减规律无法使用单一衰
减指数进行描述,需进行分段描述。
(2) 随着柱形装药长径比增加,爆炸应力波峰值应力衰减加快,衰减指数呈线性递增,近流体区和压
碎区衰减系数呈指数递减,过渡区和破裂区衰减系数呈线性递减;此外,柱形装药长径比增加导致法向
近流体区、压碎区、过渡区和破裂区范围逐渐减小。
(3) 基于混凝土介质中爆炸应力波衰减规律的分析,综合考虑了各破坏分区的差异性、装药长径比
以及埋置深度等因素,提出了柱形装药爆炸应力波峰值应力实用化计算公式,可以准确快速地计算出柱
形装药爆炸应力波的峰值应力。
参考文献:
[1] KRAUTHAMMER T. Modern protective structures [M]. Boca Raton: CRC Press, 2008. DOI: 10.1201/9781420015423.
[2] PLOOSTER M N. Blast effects from cylindrical explosive charges: experimental measurements [M]. Fort Belvoir: Defense
Technical Information Center, 1982: 11–18.
[3] ISMAIL M M, MURRAY S G. Study of the blast waves from the explosion of nonspherical charges [J]. Propellants,
Explosives, Pyrotechnics, 1993, 18(3): 132–138. DOI: 10.1002/prep.19930180304.
[4] WU C Q, FATTORI G, WHITTAKER A, et al. Investigation of air-blast effects from spherical-and cylindrical-shaped
charges [J]. International Journal of Protective Structures, 2010, 1(3): 345–362. DOI: 10.1260/2041-4196.1.3.345.
[5] SHI Y C, WANG N, CUI J, et al. Experimental and numerical investigation of charge shape effect on blast load induced by
near-field explosions [J]. Process Safety and Environmental Protection, 2022, 165: 266–277. DOI: 10.1016/j.psep.2022.
07.018.
[6] 黄家蓉, 刘光昆, 吴飚, 等. 爆炸冲击作用下混凝土中动态应力波测试与模拟 [J]. 防护工程, 2020, 42(4): 23–28. DOI:
10.3969/j.issn.1674-1854.2020.04.003.
092202-15