Page 96 - 《振动工程学报》2025年第9期

2026 振 动 工 程 学 报 第 38 卷

×10 6 6
10 ZFFT
9 D=100 D=50 5
8 FFT FFT
7 6 M-ZFFT M-ZFFT 4
计算量 5 4 幅值 3 2

3
1
2
1 0
0 1 2 3 4 5 6 7 8 9 10
0 2000 4000 6000 8000 10000 频率 / Hz

分析点数N
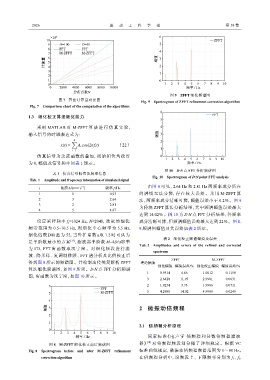
图 9 ZFFT 细化频谱图

图 7 算法计算量对比图
Fig. 9 Spectrogram of ZFFT refinement correction algorithm
Fig. 7 Comparison chart of the computation of the algorithms

6
1.3 细化校正算法细化能力 FFT
5
采用 MATLAB 对 M-ZFFT 算 法 进 行 仿 真 实 验 ， 4
输入信号的时域表达式为： 幅值 3
4 ∑ 2
x(t) = A i cos(2πf i t) （22）
1
i=1
仿真信号为余弦函数的叠加，初始相位均设置 0
1 2 3 4 5 6 7 8 9 10
为 0，幅值及信号频率如表 1 所示。 频率 / Hz

图 10 D·N 点 FFT 分析频谱图
表 1 仿真信号幅值及频率信息
Fig. 10 Spectrogram of D·N point FFT analysis
Tab. 1 Amplitude and frequency information of simulated signal

−1
i 幅值 A/(mm·s ) 频率 f /Hz 由图 8 可见，2.64 Hz 和 2.81 Hz 两频率成分所在
1 1 0.93 的谱线无法分辨，存在较大误差。采用 M-ZFFT 算
2 3 2.64 法，两频率成分清晰可辨，幅值误差小于 0.2％。图 9
3 2 2.81
为传统 ZFFT 算法分析结果，其中频谱幅值误差最大
4 5 4.87
达到 14.02％。图 10 为 D·N 点 FFT 分析结果，各频率
设定采样频率 f s =1024 Hz，N=2048，选取的细化 成分清晰可辨，但频谱幅值误差最大达到 22％。图 8、
频带范围为 0.5~10.5 Hz，则细化中心频率为 5.5 Hz， 9 频谱图幅值及其误差如表 2 所示。

细化倍数 D取整为 52，当外扩系数 a取 1.2 时可认为
表 2 细化校正频谱幅值及误差
是半阶数最小的方案 [17] ，滤波器半阶数 M=4D/ a取整
Tab. 2 Amplitudes and errors of the refined and corrected
为 173，FFT 窗函数取汉宁窗。对细化频段进行滤
spectrum
波、降采样、复调制移频、FFT 谱分析及比值校正后
ZFFT M-ZFFT
得到图 8 所示的频谱图。并绘制出传统复解析 ZFFT 理论幅值
细化幅值 幅值误差/% 细化校正幅值 幅值误差/%
算法细化频谱图，如图 9 所示。D·N 点 FFT 分析频谱
1 0.9514 4.86 1.0012 0.1150
图，窗函数为汉宁窗，如图 10 所示。
3 2.6420 11.93 2.9981 0.0631

6 2 1.9254 3.73 1.9986 0.0711
FFT
5 M-ZFFT 5 4.2988 14.02 4.9988 0.0249

4
幅值 3 2 微 振 动 倍 频 程
2

1
2.1 倍频程分析原理
0
1 2 3 4 5 6 7 8 9 10
频率 / Hz 国 家 标 准《 电 声 学 倍 频 程 和 分 数 倍 频 程 滤 波
[18]
图 8 M-ZFFT 细化校正前后频谱图 器》 对倍频程频段划分做了详细规定。根据 VC
Fig. 8 Spectrogram before and after M-ZFFT refinement 标准曲线规定，微振动倍频程频谱范围为 1～80 Hz。
correction algorithm 在倍频程分析中，设频段上、下限频率分别为 f 1 、f 2 ，