Page 51 - 《振动工程学报》2025年第9期

第 9 期 曹徐阳，等：非平稳随机主余震序列下工程结构易损性计算方法的适用性研究 1981

中位值，表 2 展示了考虑非平稳随机余震后各极限
混凝土纤维 f c
ε 状态地震易损性曲线的中位值，表 展示了考虑非
y 未约束 3
约束
z 混凝土本构 平稳随机余震后各地震水准超越概率的变化幅度。
σ
ε
钢筋纤维 总体而言，三种易损性计算方法得到的结果相
积分点 纤维截面 钢筋本构
似，发展趋势与分布范围较为一致，这也在一定程度
主节点 证明了这三种方法的有效性。对于该 3 跨 6 层钢筋
混凝土框架，当仅考虑非平稳随机主震时，通过蒙特
非线性梁柱单元
等自由度连接 节点单元 卡罗法计算得到的各极限状态下的易损性曲线中位
Y
X 值分别为 0.103g (OP)、0.468g (IO)、0.821g (LS) 和 1.534g

图 3 基于 OpenSees 的钢筋混凝土框架结构的建模方法 (CP)。对于 OP 和 IO 极限状态，最大似然估计法计
Fig. 3 Modeling strategy of reinforced concrete frames based 算得到的结果具有较好的精度，其与蒙特卡罗法的
on OpenSees 误差分别为 和 1.28%；对于 极限状态，最大
1.49% LS
在本次分析中，根据文献 [38] 选取四个极限状 似然估计法计算得到的结果仍然具有较好的精度，

态，分别为 OP 极限状态、IO 极限状态、LS 极限状态 0 ln(θ max )=1.15108·ln(PGA)−3.76002
−1
和 CP 极限状态，选择的地震动强度指标为非平稳随 β d|IM =0.591
−2
机主震的峰值加速度（PGA），工程需求参数为最大
−4
层间位移角；对于上述四个极限状态，相应的损伤指 ln(θ max ) −3
标 也 选 用 最 大 层 间 位 移 角， 相 应 的 阈 值 分 别 取 为 −5
−6 3×6 RCF
0.2%、1%、2% 和 4%。采用增量动力分析进行结构 散点
−7 线性拟合
线性拟合±对数标准差
的时程响应计算，非平稳随机主震的峰值加速度由 −8
0.1g 开始按 0.1g 的间隔逐次递增至 2.0g；对于线性拟 −3 −2 −1 0 1 2
ln(PGA)
合法及最大似然估计法，各峰值加速度水准下得到 (a) 线性拟合法
200 组数据点，该数据点分别对应 200 组非平稳随机 (a) Linear regression
主余震序列的结果，其中的变量 Θ 1 和 Θ 2 取值通过拉
丁超立方抽样得到 [39] ；对于蒙特卡罗计算法，各峰值 CP极限状态
加速度水准下得到 10000 组数据点，该数据点分别 3×6 RCF
4000
对应 10000 组非平稳随机主余震序列的结果，其中 ∂lnQ (λ, β)/∂β 6000
的变量 Θ 1 和 Θ 2 取值通过蒙特卡罗抽样得到。在计 2000
算过程中，分别计算仅考虑随机主震的响应结果以 0
及考虑随机主余震序列的响应结果，用以分析随机 0.5
0.4 2
余震对于结构性能的影响。 0.3 0 1
β 0.2 −1 lnλ
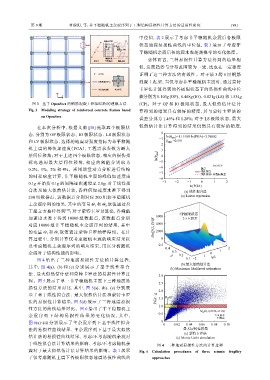
图 4 给出了三种地震易损性方法的计算过程， 0.1 −2
(b) 最大似然估计法
其 中， 图 4(a)、 (b) 和 (c) 分 别 展 示 了 基 于 线 性 拟 合 (b) Maximum likelihood estimation
法、最大似然估计法和蒙特卡罗法的易损性计算过 3.0
程。图 5 展示了单一非平稳随机主震下三种地震易
2.5
损性方法的结果对比，其中，图 5(a)、(b)、(c) 分别展
2.0
示了基于线性拟合法、最大似然估计法和蒙特卡罗 M tol (a)
法的易损性计算结果，图 5(d) 展示了三种地震易损 PGA / g 1.5
1.0
性方法的曲线结果对比。图 6 给出了非平稳随机主
M δc (a), δ c =0.02, a=1.0g
余 震 序 列 下 结 构 易 损 性 结 果 的 变 化 情 况， 其 中 ， 0.5 3×6 RCF
散点
图 6(a)~(d) 分别展示了主余震序列下基于线性拟合 0 0 0.02 0.04 0.06 0.08 0.10
法的易损性曲线结果、主余震序列下基于最大似然 最大层间位移角
(c) 蒙特卡罗法
估计法的易损性曲线结果、考虑/不考虑随机余震对 (c) Monte Carlo simulation

于线性拟合法计算结果的影响、考虑/不考虑随机余 图 4 三种地震易损性方法的计算过程
震对于最大似然估计法计算结果的影响。表 1 展示 Fig. 4 Calculation procedures of three seismic fragility
了仅考虑随机主震下各极限状态地震易损性曲线的 approaches