Page 136 - 摩擦学学报2025年第4期

624 摩擦学学报（中英文） 第 45 卷

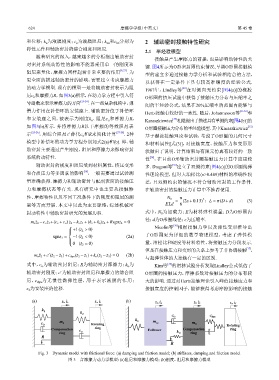
和位移；k 为液膜刚度；c 为液膜阻尼；k 和c 分别为 2 辅助密封接触特性研究
so
so
z
z

弹性元件和辅助密封的综合刚度和阻尼.
2.1 半经验模型
随着研究的深入，越来越多的分析指出辅助密封
接触是产生摩擦力的前提，也是影响动特性的关
对密封系统动特性的影响不能再采用单一的刚度和
键. 图4所示为O形密封圈约束情况.早期O形圈接触模
阻尼来量化，摩擦力同样起着非常重要的作用 [8,22] . 为
型的建立多通过接触力学分析和试验相结合的方法，
更全面的描述辅助密封的影响，需要建立考虑摩擦力
以获得在一定条件下具有较高准确度的经验公式.
的动力学模型. 现有的模型一是将辅助密封表示为阻 1967年，Lindley等 [30] 在对侧向无约束[图4(a)]的橡胶
尼c 和摩擦力R，如图3(a)所示，在动力学方程中引入符 O形圈的挤压试验中获得了接触压力分布与压缩率之
o
号函数来表示摩擦力的方向 [23-24] . 在一些复杂机构中，弹 间的半经验公式，结果在20%压缩率的范围内能够与
簧力作用在补偿环的安装座上. 辅助密封位于补偿环 Hertz接触有较好的一致性. 随后，Johannesson等 [31-32] 和
和安装座之间，被表示为刚度k 、阻尼c 和摩擦力R， Karaszkiewicz 相继提出了描述具有单侧约束[图4(b)]的
[33]
o
o
如图3(b)所示. 并将摩擦力R以干摩擦的等效阻尼表 [33]
O形圈接触压力分布的半经验模型. 其中Karaszkiewicz
示 [25-26] ，用综合阻尼 c 替代c 和R来简化计算 [27-28] . 2种
′
o 基于赫兹接触理论和试验，考虑了O形圈的几何尺寸
模型中补偿环的动力学方程分别如式2(a)和(b). 即，辅 和材料属性[式(3)]，对接触宽度、接触压力和变形形
助密封主要通过产生刚度、阻尼和摩擦力来影响密封 状做出了说明，计算结果与有限元仿真有较好的一致
系统的动特性. 性 ，在目前O形辅助密封圈接触压力计算中应用较
[34]
辅助密封的刚度和阻尼受到材料属性、挤压变形 多. Dragoni等 建立了双侧约束[图4(c)]的O形圈线弹
[35]
[29]
和介质压力等多因素的影响 ，一般需要通过试验测 性理论模型，但对大泊松比(υ>0.489)材料的准确性较
量准确获得. 摩擦力和辅助密封与配副表面的接触压 差，且双侧约束的情况不符合辅助密封的工作条件.
力和摩擦状态等有关. 现有研究中也主要从接触特 在辅助密封的接触压力计算中不推荐使用.
性、摩擦特性以及不同工况条件下的刚度和阻尼的测 N 0 π
2
= (2ε+0.13) ；L = π(D+d) (3)
量等方面开展. 本文中以此为主要脉络，综述机械密 ELd 6
封动特性中辅助密封研究的发展历程. 式中，N 为加载力；E为材料弹性模量；D为O形圈内
0
径；d为O形圈线径；ε为压缩率.
m s ¨z 2 −c z ˙z 1 +(c z +c o ) ˙z 2 −k z z 1 +(k z +k s )z 2 +Rsgn˙z 2 = 0
[36]
 Nicolin等 根据接触力学以及弹性变形推导出
+1(˙z 2 > 0)

sgn˙z 1 = −1(˙z 2 < 0) (2a) 了O形圈更为详细的数学物理模型，考虑了弹性模

 量、泊松比和硬度等材料特性，将接触压力分段表示.
0 (˙z 2 = 0)
[37]
但是在接触压力和变形的关系上参考了非协调接触 ，
m s ¨z 2 +c (˙z 2 − ˙z 3 )+c dyn (z 2 −z 1 )+k o (z 2 −z 3 ) = 0 (2b)
′
与超弹性体的大接触有一定的区别.
式中，c 为辅助密封阻尼；R为辅助密封摩擦力；k 为 Kim等 的滑移试验分析发现Lindley公式低估了
[38]
o
o
辅助密封刚度； c 为辅助密封阻尼和摩擦力的综合阻 O形圈的接触压力，摩擦系数对接触压力的分布有较
′
尼，c dyn 为无惯性黏弹性层，用于表示液膜的作用； 大的影响. 通过对Hertz接触理论引入峰值接触应力和
z 为安装座的位移. 接触宽度的控制因子，能够获得考虑摩擦影响的接触
3

(a) z 2 , z 2 z 1 , z 1 (b) z 3 , z 3 · z 2 , z 2 z 1 , z 1 ·
·
· ·
k S
k Z
c O c dyn
k S
m S m sp
c O Rotating m S Rotating
Compensation ring Follower Compensation ring
ring c Z k O ring
R
R
Fig. 3 Dynamic model with frictional force: (a) damping and friction model; (b) stiffness, damping and friction model
图 3 含摩擦力动力学模型：(a)阻尼和摩擦力模型；(b)刚度、阻尼和摩擦力模型