Page 126 - 《摩擦学学报》2021年第5期

第 5 期 王大刚, 等: 考虑微动磨损的钢丝微动疲劳裂纹扩展寿命预测研究 715

20 得微动疲劳断裂后疲劳钢丝椭圆状裂纹前缘尺寸和
5 000
10 000 最大裂纹深度(表2).
20 000
16

Wear depth/10 −3 mm 12 8 40 000 应力强度因子幅值ΔK间关系符合Paris公式[式(5) [29-30] ].
35 000
3.2 微动疲劳裂纹扩展预测理论
50 000
在裂纹扩展寿命预测时，裂纹扩展速率da/dN与
4 本文中采用有限元法开展钢丝微动疲劳裂纹扩展预
测时，通过虚拟裂纹闭合技术易于获得微动疲劳过程
0 疲劳钢丝裂纹尖端能量释放率，不同裂纹型式疲劳钢
0.0 0.2 0.4 0.6
Distance/mm 丝裂纹尖端能量释放率与应力强度因子间关系式见

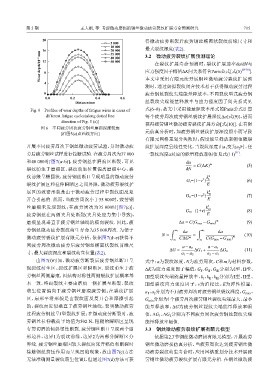
Fig. 6 Profiles of wear depths of fatigue wires in cases of 式(6~8)，故文中采用能量释放率形式的Paris公式计算
different fatigue cycles[along dotted line 每个疲劳周次疲劳钢丝裂纹扩展深度Δa[式(9)]，进而
direction of Fig. 5 (a)]
获得疲劳钢丝微动疲劳裂纹扩展寿命[式(10)]. 在有限
图 6 不同疲劳周次疲劳钢丝磨损深度轮廓
元仿真分析时，如疲劳钢丝裂纹扩展深度很小而导致
[沿图5(a)点画线方向]
有限元网格重划分失败时，假设能量释放率幅值随裂
开展不同疲劳周次下钢丝微动疲劳试验，并对微动疲 纹扩展深度呈线性变化，当裂纹深度由a 变为a 时，任
2
1
[31]
劳后疲劳钢丝试样进行拉断试验. 在疲劳周次为37 000 一裂纹深度a对应的能量释放率幅值见式(11) .
和40 000时[图7(a~b)]，疲劳钢丝在磨痕区断裂，可见 da
= C(∆K) m (5)
裂纹萌生于磨痕区、裂纹萌生位置偏离磨痕中心，裂 dN
纹前缘呈椭圆状，疲劳钢丝断口呈现明显的微动疲劳 k 2
2
G I =(1−ν ) I (6)
裂纹扩展区和拉伸瞬断区之间界限，微动疲劳裂纹扩 E
展区的致密形貌是由于微动疲劳过程中裂纹面反复 k 2
2
G II =(1−ν ) II (7)
开合引起的. 然而，当疲劳周次小于35 000时，疲劳钢 E
丝磨痕未发现裂纹；在疲劳周次为35 000时[图7(c)]， k 2
G III =(1+ν) III (8)
疲劳钢丝在两侧夹具处断裂(夹具处应力集中导致)， E
磨痕呈现垂直于疲劳钢丝轴线的横向裂纹. 因此，疲 ∆a = C(G max −G min ) m (9)
劳钢丝微动疲劳裂纹萌生寿命为35 000周次. 为便于 ∫ a 2 da ∫ a 2 da
N = = (10)
微动疲劳裂纹扩展有限元分析，依据图7(d~e)获得不 C∆G m C(G max −G min ) m
a 1 a 1
同疲劳周次微动疲劳后疲劳钢丝椭圆状裂纹前缘尺
∆G = a−a 2 ∆G 1 + a−a 1 ∆G 2 (11)
寸、最大裂纹深度和裂纹萌生位置(表2). a 1 −a 2 a 2 −a 1
由图7(f)可知，微动疲劳断裂后疲劳钢丝断口呈 式中：a为裂纹深度，N为疲劳周次，C和m为材料参数，

现裂纹萌生区、裂纹扩展区和瞬断区. 裂纹萌生于疲 ΔK为应力强度因子幅值，G 、G 、G 分别为I型、II型、
I
II
III
劳钢丝两侧磨痕，因结构对称性两侧裂纹扩展概率基 III型裂纹尖端能量释放率，k 、k 、k 分别为I型、II型、
III
II
I
本一致，终而裂纹主要由磨痕一侧扩展至断裂，裂纹 III型裂纹应力强度因子，v为泊松比，E为弹性模量，
萌生位置偏向于疲劳钢丝磨痕疲劳侧；在裂纹扩展 a 、a 分别为不同疲劳周次时疲劳钢丝裂纹深度，G max 、
2
1
区，扇形平滑形貌是由裂纹面反复开合和摩擦引起 G min 分别为1个疲劳周次疲劳钢丝裂纹尖端最大、最小
的，裂纹面近似垂直于疲劳钢丝轴线，表明微动疲劳 能量释放率，ΔG为疲劳钢丝裂纹尖端能量释放率幅
过程疲劳钢丝呈I型裂纹扩展；在微动疲劳断裂时，疲 值，ΔG 、ΔG 分别为不同疲劳周次疲劳钢丝裂纹尖端
2
1
劳钢丝拉伸载荷平均值为502 N，粗糙的瞬断区呈现 能量释放率幅值.

有剪切唇的倾斜塑性断裂. 疲劳钢丝断口呈现两个扇 3.3 钢丝微动疲劳裂纹扩展有限元模型
形边界，边界1为裂纹前缘、边界2为两部分瞬断区分 依据第2.3节钢丝微动磨损有限元模型，开展疲劳
界线. 疲劳钢丝磨痕因较大裂纹面张开幅值和断裂时 钢丝微动磨损仿真分析，当疲劳周次达到疲劳钢丝微
接触钢丝挤压作用而呈现凹陷现象，故由图7(e)方法 动疲劳裂纹萌生寿命时，应用网格重划分技术开展疲
无法准确测量裂纹萌生位置l，但通过图7(d)方法可获 劳钢丝微动疲劳裂纹扩展有限元分析. 在钢丝微动疲