Page 124 - 《摩擦学学报》2021年第5期

第 5 期 王大刚, 等: 考虑微动磨损的钢丝微动疲劳裂纹扩展寿命预测研究 713

量表征疲劳钢丝磨痕轮廓尺寸，获得磨痕轮廓的椭圆 元模型(图4)，为提高收敛性和计算效率，忽略微动疲
拟合曲线以及椭圆长轴和短轴的长度值. 图2(b)给出 劳过程中塑性变形效应，将疲劳钢丝和加载钢丝均设
了不同疲劳周次时椭圆形磨痕轮廓长轴和短轴的长 为弹性各向同性材料；依据第1节对各钢丝施加材料
度值，发现两者均随疲劳周次增加而逐渐增大. 图3给 参数，试设疲劳钢丝磨损系数K =1×10 mm /(N·mm) ，
[24]
3
−8
s
出了微动疲劳过程中钢丝间摩擦系数演化曲线，发现 通过试验结果进行修正；采用迭代计算方法，设1个迭
钢丝间摩擦系数呈现先增加后稳定的变化趋势，稳定 代循环对应疲劳周次ΔN=500 . 在有限元模型中，设
[18]
值约0.55. 置节点对面段(Node To Segment)接触控制方法和双
线性库仑摩擦模型，依据第2.1节稳定阶段钢丝间摩擦

0.8
系数设置钢丝间摩擦系数为0.55，约束疲劳钢丝一端
所有自由度，允许加载钢丝沿垂直于疲劳钢丝轴线方
0.6
Friction coefficient 0.4 向运动及疲劳钢丝另一端轴向运动，约束加载钢丝和
疲劳钢丝另一端其他自由度，通过面载荷法施加钢丝
间接触载荷35 N和疲劳钢丝另一端疲劳载荷150~550 N.
0.2
运用八节点六面体单元对疲劳钢丝和加载钢丝进行
网格划分，依据优化网格准则定义钢丝接触区网格尺
0.0 [17-18, 24, 26]
0 5 10 15 寸，即接触区网格尺寸为磨痕尺寸3%～5%范围内 ，
Time/10 s
3
由图2(b)发现疲劳钢丝磨痕尺寸范围250～400 μm，故
Fig. 3 Friction coefficient between contacting wires during the 局部接触区细化网格尺寸设为20 μm×20 μm，有限元
fretting fatigue test
图 3 微动疲劳过程中接触钢丝间摩擦系数演化 模型的单元数和节点数分别为89 850和98 268.

2.2 微动磨损理论 Mesh refinement
region
在微动磨损仿真过程中，通过式(1)计算疲劳钢丝 Loading wire
磨损体积 [21, 24] ；微动磨损后，钢丝局部接触区可认为是
平面接触，对式(1)两侧同时除以接触面积A 可得式(2)，
c
·
对式(2)微分可得式(3)，即 h为1个增量步疲劳钢丝局 Fatigue wire
部接触区磨损深度变化率，n个增量步后疲劳钢丝局
[25]
部接触区总磨损深度见式(4) . 为了提高计算效率，
假设ΔN疲劳周次为1个迭代循环(增量步)以及每个迭 Loading wire
代循环局部接触区的接触应力和相对滑移均为恒定
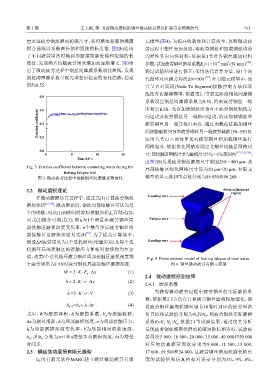
值，故第i个迭代循环疲劳钢丝局部接触区磨损深度等 Fig. 4 Finite element model of fretting fatigue of steel wires
于疲劳周次为i·ΔN时疲劳钢丝局部接触区磨损深度. 图 4 钢丝微动疲劳有限元模型

W = 2· K · F n ·∆x (1)
2.4 微动磨损预测结果

h = 2· K ·σ·∆x (2)
2.4.1 磨损系数
· 为获得微动疲劳过程中疲劳钢丝的实际磨损系
h =2· K ·σ·V (3)
数，依据第2.3节仿真计算疲劳钢丝磨痕轮廓演化，假
·
h n+1 =h n + h ·∆t (4) 设疲劳钢丝磨痕轮廓短轴长相等时对应的疲劳周次
式中：W为磨损体积，K为磨损系数，F 为接触载荷， 仿真值和试验值分别为N 和N ，则疲劳钢丝实际磨损
n
e
s
Δx为相对滑移，h为局部磨损深度，σ为局部接触压力， 系数K=K ·N /N . 依据2.1节试验结果，通过仿真分析
e
s
s
·
h为局部磨损深度变化率，V为局部相对滑移速度， 发现疲劳钢丝椭圆状磨痕轮廓短轴长相等时，试验疲
h n+1 和h 分别为n+1和n增量步总磨损深度，Δt为增量 劳周次5 000，10 000，20 000，35 000，40 000和50 000
n
时间步. 对应的仿真疲劳周次分别为9 000、11 500、15 000、

2.3 钢丝微动磨损有限元模型 17 000、19 500和24 000，且疲劳钢丝磨痕轮廓长轴长
运用有限元软件MARC建立钢丝微动疲劳有限 度的试验值和仿真值相对误差分别为8%、9%、4%、