Page 125 - 《摩擦学学报》2021年第5期

714 摩 擦 学 学 报 第 41 卷

1.300e-02 Wear scar profile 1.300e-02 1.300e-02
1.156e-02 1.156e-02 1.156e-02
1.011e-02 1.011e-02 1.011e-02
8.667e-03 8.667e-03 8.667e-03
7.222e-03 7.222e-03 7.222e-03
5.778e-03 5.778e-03 5.778e-03
4.333e-03 4.333e-03 4.333e-03
2.889e-03 2.889e-03 2.889e-03
1.444e-03 1.444e-03 1.444e-03
0.000e+00 0.000e+00 0.000e+00
(a) 9 000 cycles (b) 11 500 cycles (c) 15 000 cycles

1.300e-02 1.300e-02 1.300e-02
1.156e-02 1.156e-02 1.156e-02
1.011e-02 1.011e-02 1.011e-02
8.667e-03 8.667e-03 8.667e-03
7.222e-03 7.222e-03 7.222e-03
5.778e-03 5.778e-03 5.778e-03
4.333e-03 4.333e-03 4.333e-03
2.889e-03 2.889e-03 2.889e-03
1.444e-03 1.444e-03 1.444e-03
0.000e+00 0.000e+00 0.000e+00
(d) 17 000 cycles (e) 19 500 cycles (f) 24 000 cycles

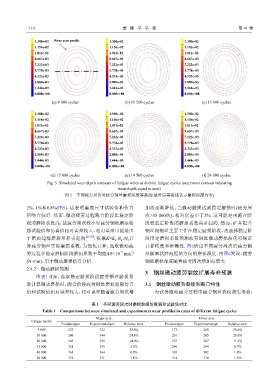
Fig. 5 Simulated wear depth contours of fatigue wires at distinct fatigue cycles (outermost contour indicating
wear depth equal to zero)
图 5 不同疲劳周次时疲劳钢丝磨损深度等高线(最外层等高线表示磨损深度为零)

2%、1%和0.8%(图5)，这表明磨痕尺寸试验值和仿真 加而逐渐降低，当微动磨损达到稳定磨损时(疲劳周

值吻合较好. 然而，微动疲劳过程跑合阶段比稳定阶 次>35 000次)，相对误差小于5%. 这可能是由跑合阶
段的磨损系数高，故疲劳周次较小时疲劳钢丝磨痕轮 段较稳定阶段的磨损系数高引起的. 然而，矿井提升
廓试验值和仿真值相对误差较大，相对误差可能是由 钢丝绳钢丝主要工作在稳定磨损阶段，故选择稳定阶
于磨痕边缘磨屑堆积引起的 [27-28] . 依据K=K ·N /N 计 段恒定磨损系数预测疲劳钢丝微动磨损演化可保证
s
s
e
算疲劳钢丝实际磨损系数，为简化计算，选取微动疲 计算精度和准确性. 图6给出不同疲劳周次沿疲劳钢
−9 3
劳过程中稳定磨损阶段磨损系数平均值4.8×10 mm / 丝椭圆状磨痕短轴方向的磨损深度，由图6发现，疲劳
(N·mm)，用于微动磨损仿真分析. 钢丝磨损深度随着疲劳周次增加而增大.

2.4.2 微动磨损预测
3 钢丝微动疲劳裂纹扩展寿命预测
由表1可知，选取稳定磨损阶段疲劳钢丝磨损系
数计算微动磨损时，跑合阶段疲劳钢丝磨痕轮廓仿真 3.1 钢丝微动疲劳裂纹和断口特性
值和试验值相对误差较大，相对误差随着疲劳周次增 为获得微动疲劳过程中疲劳钢丝裂纹萌生寿命，

表 1 不同疲劳周次时磨损轮廓仿真值和试验值对比
Table 1 Comparisons between simulated and experimental wear profiles in cases of different fatigue cycles

Major axis Minor axis
Fatigue cycles
Predicted/μm Experimental/μm Relative error Predicted/μm Experimental/μm Relative error
5 000 223 322 30.8% 177 248 28.6%
10 000 260 344 24.4% 210 265 20.8%
20 000 303 356 14.9% 255 287 11.2%
35 000 351 359 2.2% 296 294 0.7%
40 000 361 364 0.8% 305 302 1.0%
50 000 375 371 1.1% 314 310 1.3%