Page 29 - 《摩擦学学报》2021年第3期

318 摩 擦 学 学 报 第 41 卷

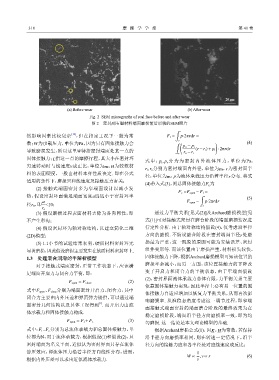
10 μm 20 μm

(a) Before wear (b) After wear

Fig. 2 SEM micrographs of seal face before and after wear
图 2 密封副石墨材料端面磨损前后形貌的SEM照片
∫
[10]
然影响因素比较复杂 ，但在指定工况下一般为常 F l = p·2πrdr =
r
数； W为承载压力，单位为 Pa，因为只有固体接触力会 ∫ ( ) (4)
p o − p i
导致磨损发生，所以这里 W特指密封端面处某一点的 (r −r i )+ p i ·2πrdr
r r o −r i
固体接触力； L指这一点的摩擦行程，其大小在密封环 式中： p i , p o 分为为密封内外流体压力，单位为Pa，
匀速转动时与线速度 v成正比，单位为 ； 为较软材
m H
r i ,r o 分别为密封端面内外径，单位为 ， 为密封面半
m r
料的表面硬度，一般由材料本身性质决定. 即在公式
m p为液体承载压力沿着半径 分布. 将式
径，单位为 ， r
适用的条件下，磨损只和线速度及接触压力有关；
(4)带入式(3)，则总固体接触力F 为
c
(2) 接触式端面密封多为窄端面设计以减小发
F c =F open − F l =
热，假设密封环面满足端面宽度a远远小于密封环半 ∫ (5)
a F open − p·2πrdr
径 r 0，即 <10； r
r o
(3) 假设磨损过程表面材料去除为各向同性，即 通过力平衡关系[见式(2)]及Archard磨损模型[见
不产生犁沟； 式(1)]可对接触式密封在磨合阶段的端面磨损情况进
(4) 假设密封环为轴对称结构，以建立简化二维 行定性分析. 由于轴对称结构假设(4)，仅考虑沿半径
(2D)模型； 方向的磨损. 不妨设磨合阶段在密封端面半径 r 处磨
(5) 1.1小节的试验结果表明，硬质材料密封环无 损最为严重，这一现象的原因可能为安装误差、密封
组件变形等. 而该位置由于磨损严重，材料损失较快，
显著磨损，因此假设磨损主要发生在软质材料密封环上.

1.3 处理混合润滑的半解析模型 固体接触力下降，根据Archard磨损模型可知该位置的
对于接触式端面密封，正常工作状态下，应该满 磨损率会减小；而另一方面，该位置接触力的下降改
足端面开启力与闭合力平衡，即： 变了开启力和闭合力的平衡状态，由于窄端面假设
(2)，密封界面流体承载力总体有限，力平衡关系主要
(2)
F open = F close
依靠固体接触力实现，因此半径上必有另一位置的固
、
式中 F open F close 分别为端面密封开启力、闭合力，其中
体接触力自适应增加以恢复力平衡关系，从而再次影
闭合力主要由内外压差和弹簧弹力提供，可以通过端
响磨损率. 从准稳态角度考虑这一调节过程，即窄端
[1]
面密封几何结构以及具体工况得到 . 而开启力由流
面接触式端面密封的端面磨合阶段的最终效果为在
体承载力和固体接触力构成.
稳定磨损阶段，端面沿半径方向磨损率一致，即为均
(3)
F open = F l + F c
匀磨损. 这一结论是本文理论模型的基础.
式中： 、 根据Archard磨损公式(1)，因 ，
F l F c 分别为总流体承载力和总固体接触力，单
K H为常数，若保持
位都为N，对于流体承载力，根据假设(1)和假设(2)，且 沿半径方向磨损率相同，则在转速一定情况下，沿半
密封端面为名义平面，近似认为密封界面只存在流体 径方向的接触力应和各半径处对应线速度成反比：
静压效应，即流体压力沿着半径方向线性分布，进而， 1
W ∝ ,v ∝ r (6)
根据内外压差可以求出近似流体承载力. v