Page 34 - 《摩擦学学报》2021年第3期

惠玉祥, 等: 考虑磨损的接触式端面密封模型及试验
第 3 期 Exp-2-1 Exp-2-2 Exp-2-4 Exp-1-4 5.00 Experiemnt X-1 4.36 323
Real-time temperature of end face, T/℃ 200 Theoretical Exp-2-3 Exp-1-1 Exp-1-4 Leakage quantity, Q/(mL/h) 4.00 3.23 3.15 2.45 3.65 2.09 4.06 3.95 3.34
250
4.50
Experiemnt X-2
calculation
3.50
150
3.00
2.50
Exp-1-2
100
2.00
1.50
50
0.50
Stable wear stage
0
0.00
360
0 Acceleration stage 720 900 1 080 1 260 1 440 1 620 1.00
180
540
Experiemnt X-2
Experiemnt X-4
Experiment time, t/s Experiemnt X-1 Experiemnt X-3 Theoretical
calculation
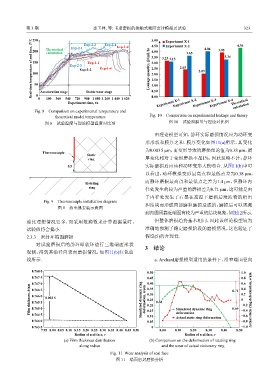
Fig. 8 Comparison on experimental temperature and
theoretical model temperature Fig. 10 Comparison on experimental leakage and theory
图 8 试验温度与理论模型温度对比图 图 10 试验泄漏量与理论对比图
由理论模型可知，静环实际磨损情况应为动环变
形形状和膜厚之和. 膜厚变化如图11(a)所示，其变化
为0.003 5 μm，而变形导致的磨损理论值为0.38 μm，膜
Thermocouple
Static
ring 厚变化相对于变形磨损不足1%，因此忽略不计，静环
0.5 实际磨损后应该和动环变形大致吻合. 从图11(b)中可
以看出，动环模拟变形最高点和最低点差为0.38 μm，
而静环磨损最高点和最低点之差为1.4 μm，但静环内
Rotating
ring
径处发生的较为严重的磨损差为0.71 μm，这可能是由
于内径处发生了石墨在高温下磨损后浸渍物的析出

Fig. 9 Thermocouple installation diagram
和结块而形成局部磨粒磨损造成的，磨损后可以观测
图 9 热电偶安装示意图
到内圆周靠近端面有较为严重的结块现象，如图12所示.
油比理想情况要多，而采用数滴数来计算泄漏量时， 但整体磨损趋势基本相同，因此该理论模型较为
试验值将会偏小. 准确地预测了稳定磨损阶段的磨损情况，这也验证了

2.3.3 密封环端面磨损 假设(5)的合理性.

对试验磨损后的静环即软环进行三维端面形状
3 结论
观测，得到其沿径向表面磨损情况，如图11(b)红色曲
线所示. a. Archard磨损模型适用的条件下，沿窄端面径向

0.768 0
0.50 1.0
0.767 5 0.45 0.8
0.767 0 0.40 0.71 0.6
Film thickness, h/μm 0.766 0 0.003 5 Simulated dynamic ring deformation, u/μm 0.30 0.38 Simulated dynamic ring 0.69 0.2 Actual static ring deformation, u/μm
0.4
0.35
0.766 5
0
0.25
0.765 5
−0.2
0.20
0.765 0
−0.4
0.764 5
0.10
Actual static ring deformation
−0.8
0.764 0 0.15 deformation −0.6
0.05
0.763 5 0 −1.0
7.95 8.00 8.05 8.10 8.15 8.20 8.25 8.30 8.35 8.40 8.45 8.50 8.00 8.10 8.20 8.30 8.40 8.50
Radius of seal face, r Radius of seal face, r
(a) Film thickness distribution (b) Comparison on the deformation of ratating ring
along radius and the wear of actual stationary ring

Fig. 11 Wear analysis of seal face
图 11 端面密封磨损分析