Page 37 - 《摩擦学学报》2021年第1期

34 摩 擦 学 学 报 第 41 卷

0.18 0.22
F v /N F v /N
1.4 1.4
0.15 0.20
1.2 1.0
1.0 0.8
0.12 0.8
0.6 0.6
S h /S v 0.09 0.4 µ a =µ 0 −S h /S v 0.18 0.4
0.16
0.2
0.06 0.14
0.2
0.03 0.12
0.00 0.10
−4 −3 −2 −1 0 1 2 3 4 −4 −3 −2 −1 0 1 2 3 4
Tilt angle, θ/(°) Tilt angle, θ/(°)
(a) The S h /S v is calculated by Eq. (17) and (19) (b) The μ a is calculated by Eq. (11)

Fig. 12 Effect of sample tilt on the components of nominal friction coefficient under different constant normal load
图 12 不同恒定正压力下试样倾斜对名义摩擦系数中各组分的影响

0.14 0.22
F v /N
0.12 F v /N 0.20 1.4
1.4 1.0
0.10 1.2 0.18 0.8
1.0 0.6
S t /S n 0.08 0.8 µ a =µ r −S t /S n 0.16 0.4
0.6
0.4
0.06 0.14
0.2 0.2
0.04 0.12
0.02 0.10
−4 −3 −2 −1 0 1 2 3 4 −4 −3 −2 −1 0 1 2 3 4
Tilt angle, θ/(°) Tilt angle, θ/(°)
(a) The S t /S n is calculated by Eq. (22) and (23) (b) The μ a is calculated by Eq. (12)

Fig. 13 Effect of sample tilt on the components of true friction coefficient under different constant normal load
图 13 不同恒定正压力下试样倾斜对真实摩擦系数中各组分的影响

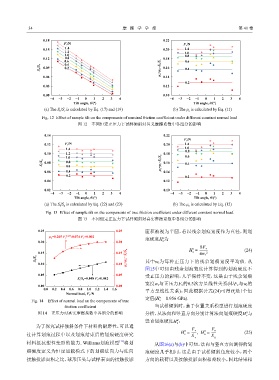
0.25 0.25 面积被视为半圆，若以残余划痕宽度作为直径，则划
0.397 -0.074 F v +0.002
痕硬度 H 为
µ a =0.265 F v
r
0.20 0.20 s
8F v
r
s
0.15 0.15 H = πw r 2 (24)
S t /S n µ a =µ 0 − S t /S n 其中 w r 为每种正压力下的残余划痕宽度平均值. 从
0.10 0.10
图15中可知由残余划痕宽度计算得到的划痕硬度不
0.05 0.05 受正压力的影响，几乎保持不变，这是由于残余划痕
S t /S n =0.048 F v +0.042
宽度 w r 与正压力 F v 的0.5次方呈线性关系(即 F v 与 的
0.00 0.00 w r
0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 平方呈线性关系)，因此根据公式(24)可得 H 是1个恒
r
Normal load, F v /N s
r
定值( H = 0.956 GPa).
Fig. 14 Effect of normal load on the components of true s
friction coefficient 当试样倾斜时，基于位置关系模型进行划痕硬度
图 14 正压力对真实摩擦系数中各组分的影响 分析，从法向和竖直方向分别计算法向划痕硬度 H 与
θ
v
竖直划痕硬度 H ：
θ
n
为了探究试样倾斜条件下材料的耐磨性，可以通
θ
θ
过计算划痕过程中以及划痕结束后的划痕硬度研究 H = F v , H = F n (25)
v
n
S
S
v n
[11]
材料抵抗塑性变形的能力. Williams划痕模型 将划 从图16(a)与(b)中可知，法向与竖直方向测得的划
痕硬度定义为恒定加载模式下的划痕法向力与法向 痕硬度几乎相同，这是由于试样倾斜角度较小，两个
接触投影面积之比，球形压头与试样表面的接触投影 方向的载荷以及接触投影面积相差较小，因此结果相