Page 35 - 《摩擦学学报》2021年第1期

32 摩 擦 学 学 报 第 41 卷

0.35 0.33
0.28
F v /N µ r =0.28 F v
0.30
1.4 0.27
Friction coefficient, µ r 0.25 0.8 Friction coefficient, µ r 0.24
0.30
1.2
1.0
0.6
0.21
0.4
0.20
0.2 0.18
0.15 0.15
−4 −3 −2 −1 0 1 2 3 4 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6
Tilt angle, θ/(°) Normal load, F v /N
(a) μ r vs θ (b) μ r vs F v

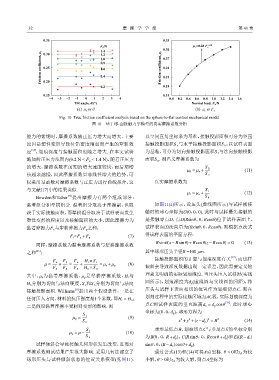
Fig. 10 True friction coefficient analysis based on the sphere-to-flat contact mechanical model
图 10 基于球-面接触力学模型的真实摩擦系数分析

能力的紫铜时，摩擦系数随正压力增大而增大，主要 以空间直角坐标系为基准，接触投影面积可分为竖直
原因是塑性变形导致位错密度增加而产生的犁耕效 接触投影面积 S v 与水平接触投影面积 S h ；以试样表面
[24]
应 ，划痕深度与接触面积也随之增大. 在本文试验 为基准，可分为切向接触投影面积 S t 与法向接触投影
施加的正压力范围内(0.2 N < F < 1.4 N)，随着正压力 面积 S n . 则名义摩擦系数为
v
的增大，摩擦系数在前期的增大速度较快，而后期增 S h
µ 0 = µ a + (11)
长越来越慢，因此摩擦系数呈非线性增大的趋势，可 S v
以采用幂函数对摩擦系数与正压力进行曲线拟合，这 真实摩擦系数为
与文献[17]中的结果类似. S t
µ r = µ a + (12)
[42]
Bowden和Tabor 提出摩擦力有两个组成部分： S n
黏着组分和犁耕组分. 黏着组分取决于摩擦副，也取 如图11(a)所示，设压头(虚线圆所示)与试样刚接
决于实际接触面积，而犁耕组分取决于试样表面发生 触时的球心坐标为O(0，0，0). 此时与试样最先接触的
塑性变形的程度以及接触面积的大小，因此摩擦力为 是接触零点D，点D(Rsinθ，0，Rcosθ)位于试样表面上，
黏着摩擦力 F a 与犁耕摩擦力 之和： 试样表面的法向量为(Rsinθ，0，Rcosθ)，则根据点法式
F p
得试样表面的平面方程：
(7)
F t =F a + F p
Rsinθ(x−Rsinθ)+Rcosθ(z−Rcosθ) = 0 (13)
同样，摩擦系数为黏着摩擦系数与犁耕摩擦系数
[43]
之和 ： 其中球形压头半径R =100 μm.
接触投影面积的计算与划痕深度有关 ，而试样
[27]
F a F p F a H t ×S t
µ = + = + = µ a +µ p (8) 倾斜会导致深度数据出现一定误差，因此需要定义物
F n F n F n H n ×S n
其中： µ a为黏着摩擦系数， 是犁耕摩擦系数， H t 与 理意义明确的实际划痕深度. 当压头压入试样时(实线
µ p
H n 分别为切向与法向硬度， 和 S n 分别为切向与法向 圆所示)，划痕深度为 d p(虚线圆与实线圆的间距)，将
S t
[11]
接触投影面积. Williams 提出两个假设条件：一是在 压头与试样下表面相切的位置作为划痕切点C，则在
任何压入方向，材料的抗压强度是1个常数，即 H t = H n ； 划刻过程中的实际接触区域为AC段，实际划痕深度为
二是假设黏着摩擦不受材料变形的影响. 则 点C到试样表面的垂直距离 d c = d p cosθ [29] . 此时球心
坐标为(0，0， d p)，球形方程为
S t
µ p = (9) 2 2 2 2
S n x +y +(z−d p ) = R (14)
球形最低点B、划痕切点C与垂足点E的坐标分别
S t
µ a = µ− (10)
为B(0，0， Rsinθ，0，
S n R+d p )、C( Rcosθ +d p )和E( (R−d c )
试样倾斜会导致接触几何形状发生改变，进而对 sinθ，0， (R−d c )cosθ +d p).
摩擦系数测试结果产生很大影响. 采用几何法建立了 通过公式(13)和(14)可得A点坐标. θ < 0时 z A 为较
球形压头与试样倾斜状态的位置关系模型(见图11). 小解，θ > 0时 z A 为较大解，则点A坐标为